Linear-Phase Filters
(Symmetric Impulse Responses)
A linear-phase filter is typically used when a causal filter is needed to modify a signal's magnitude-spectrum while preserving the signal's time-domain waveform as much as possible. Linear-phase filters have a symmetric impulse response, e.g.,
We will show that every real symmetric impulse response corresponds to
a real frequency response times a
linear phase term
![]() , where
, where
![]() is the slope of the linear phase. Linear phase is
often ideal because a filter phase of the form
is the slope of the linear phase. Linear phase is
often ideal because a filter phase of the form
![]() corresponds to phase delay
corresponds to phase delay
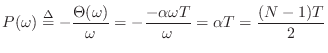
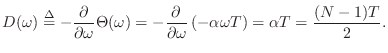
Next Section:
Zero-Phase Filters (Even Impulse Responses)
Previous Section:
Pole-Zero Analysis Problems




















