Direct Proof of De Moivre's Theorem
In §2.10, De Moivre's theorem was introduced as a consequence of Euler's identity:
Proof:
To establish the ``basis'' of our mathematical induction proof, we may
simply observe that De Moivre's theorem is trivially true for
![]() . Now assume that De Moivre's theorem is true for some positive
integer
. Now assume that De Moivre's theorem is true for some positive
integer ![]() . Then we must show that this implies it is also true for
. Then we must show that this implies it is also true for
![]() , i.e.,
, i.e.,
Since it is true by hypothesis that
From trigonometry, we have the following sum-of-angle identities:
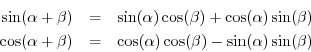
These identities can be proved using only arguments from classical
geometry.3.8Applying these to the right-hand side of Eq.![]() (3.3), with
(3.3), with
![]() and
and
![]() , gives Eq.
, gives Eq.![]() (3.2), and
so the induction step is proved.
(3.2), and
so the induction step is proved.
![]()
De Moivre's theorem establishes that integer powers of
![]() lie on a circle of radius 1 (since
lie on a circle of radius 1 (since
![]() , for all
, for all
![]() ). It
therefore can be used to determine all
). It
therefore can be used to determine all ![]() of the
of the ![]() th roots of unity
(see §3.12 above).
However, no definition of
th roots of unity
(see §3.12 above).
However, no definition of ![]() emerges readily from De Moivre's
theorem, nor does it establish a definition for imaginary exponents
(which we defined using Taylor series expansion in §3.7 above).
emerges readily from De Moivre's
theorem, nor does it establish a definition for imaginary exponents
(which we defined using Taylor series expansion in §3.7 above).
Next Section:
Euler_Identity Problems
Previous Section:
Roots of Unity




















