Digital Sinusoid Generators

In [170], three techniques were examined for generating sinusoids digitally by means of recursive algorithms.^J.1 The recursions can be interpreted as implementations of second-order digital resonators in which the damping is set to zero. The three methods considered were (1) the 2D rotation (2DR), or complex multiply (also called the ``coupled form''), (2) the modified coupled form (MCF), or ``magic circle'' algorithm,^J.2which is similar to (1) but with better numerical behavior, and (3) the direct-form, second-order, digital resonator (DFR) with its poles set to the unit circle.

These three recursions may be defined as follows:

where , , is the instantaneous frequency of oscillation (Hz) at time sample , and is the sampling period in seconds. The magic circle parameter is .

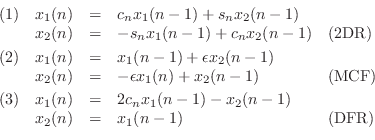
The digital waveguide oscillator appears to have the best overall properties yet seen for VLSI implementation. This structure, introduced in [468], may be derived from the theory of digital waveguides (see Appendix H, Appendix I, and [442,472]). Any second-order digital filter structure can be used as a starting point for developing a corresponding sinusoidal signal generator, so in this case we begin with the second-order waveguide filter.

---

Order a Hardcopy of Physical Audio Signal Processing

Previous: Additive Synthesis
Next: The Second-Order Waveguide Filter

---

written by Julius Orion Smith III
Julius Smith's background is in electrical engineering (BS Rice 1975, PhD Stanford 1983). He is presently Professor of Music and Associate Professor (by courtesy) of Electrical Engineering at Stanford's Center for Computer Research in Music and Acoustics (CCRMA), teaching courses and pursuing research related to signal processing applied to music and audio systems. See http://ccrma.stanford.edu/~jos/ for details.