Sign in

username:

password:



Not a member?

Search Online Books



Search tips

Free Online Books

Sponsor

Evaluate multicore with Texas Instruments:
Low-cost evaluation module & free software development kit available NOW.

Chapters

See Also

Embedded SystemsFPGAElectronics

Spectral Audio Signal Processing
    Gaussian Function Properties
       Fourier Transform of Complex Gaussian
          Alternate Proof

Chapter Contents:

Search Spectral Audio Signal Processing

  

Book Index | Global Index

Would you like to be notified by email when Julius Orion Smith III publishes a new entry into his blog?

  

Alternate Proof

The Fourier transform of a complex Gaussian can also be derived using the differentiation theorem and its dual (§B.1.2).D.1



Proof: Let

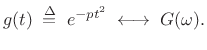$\displaystyle g(t)\isdefs e^{-pt^2} \;\longleftrightarrow\;G(\omega). $

Then by the differentiation theorem (§B.1.2),

$\displaystyle g^\prime(t) \;\longleftrightarrow\;j\omega G(\omega). $

By the differentiation theorem dual (§B.1.3),

$\displaystyle -jtg(t) \;\longleftrightarrow\;G^\prime(\omega). $

Differentiating $ g(t)$ gives

$\displaystyle g^\prime(t) \eqsp -2ptg(t) \eqsp \frac{2p}{j}[-jtg(t)] \;\longleftrightarrow\;\frac{2p}{j}G^\prime(\omega). $

Therefore,

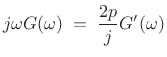$\displaystyle j\omega G(\omega) \eqsp \frac{2p}{j}G^\prime(\omega) $

or

$\displaystyle \left[\ln G(\omega)\right]^\prime \eqsp \frac{G^\prime(\omega)}{G... ...ga)} \eqsp -\frac{\omega}{2p} \eqsp \left(-\frac{\omega^2}{4p}\right)^\prime. $

Integrating both sides with respect to $ \omega$ yields

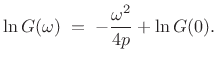$\displaystyle \ln G(\omega) \eqsp -\frac{\omega^2}{4p} + \ln G(0). $

In §D.7, we found that $ G(0)=\sqrt{\pi/p}$, so that, finally, exponentiating gives

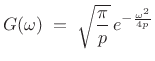$\displaystyle G(\omega) \eqsp \sqrt{\frac{\pi}{p}}\,e^{-\frac{\omega^2}{4p}} $

as expected.

The Fourier transform of complex Gaussians (``chirplets'') is used in §9.10 to analyze Gaussian-windowed ``chirps'' in the frequency domain.

Previous: Fourier Transform of Complex Gaussian
Next: Why Gaussian?

Order a Hardcopy of Spectral Audio Signal Processing

About the Author: Julius Orion Smith III
Julius Smith's background is in electrical engineering (BS Rice 1975, PhD Stanford 1983). He is presently Professor of Music and Associate Professor (by courtesy) of Electrical Engineering at Stanford's Center for Computer Research in Music and Acoustics (CCRMA), teaching courses and pursuing research related to signal processing applied to music and audio systems. See http://ccrma.stanford.edu/~jos/ for details.


Comments

No comments yet for this page


Add a Comment
You need to login before you can post a comment (best way to prevent spam). ( Not a member? )