Chebyshev Polynomials
The ![]() th Chebyshev polynomial may be defined by
th Chebyshev polynomial may be defined by
![$\displaystyle T_n(x) = \left\{\begin{array}{ll} \cos[n\cos^{-1}(x)], & \vert x\vert\le1 \\ [5pt] \cosh[n\cosh^{-1}(x)], & \vert x\vert>1 \\ \end{array} \right..$](http://www.dsprelated.com/josimages_new/sasp2/img534.png) |
(4.46) |
The first three even-order cases are plotted in Fig.3.35. (We will only need the even orders for making Chebyshev windows, as only they are symmetric about time 0.) Clearly,
| (4.47) |
for
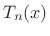 is an
is an  th-order polynomial in
th-order polynomial in  .
.
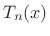 is an even function when
is an even function when  is an even integer,
and odd when
is an even integer,
and odd when  is odd.
is odd.
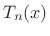 has
has  zeros in the open interval
zeros in the open interval 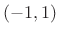 , and
, and
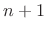 extrema in the closed interval
extrema in the closed interval ![$ [-1,1]$](http://www.dsprelated.com/josimages_new/sasp2/img543.png) .
.
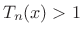 for
for 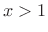 .
.
Next Section:
Dolph-Chebyshev Window Definition
Previous Section:
Kaiser and DPSS Windows Compared








![\includegraphics[width=\twidth]{eps/first-even-chebs-c}](http://www.dsprelated.com/josimages_new/sasp2/img533.png)












