Duality of COLA and Nyquist Conditions
Let
![]() denote constant overlap-add using hop size
denote constant overlap-add using hop size ![]() . Then we
have (by the Poisson summation formula Eq.
. Then we
have (by the Poisson summation formula Eq.![]() (8.30))
(8.30))
![\begin{eqnarray*}
w &\in& \hbox{\sc Nyquist}(N) \Leftrightarrow W \in \hbox{\sc Cola}(2\pi/N) \qquad \hbox{(FBS)} \\ [10pt]
w &\in& \hbox{\sc Cola}(R) \Leftrightarrow W \in \hbox{\sc Nyquist}(2\pi/R) \qquad \hbox{(OLA)}
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img1630.png)
Specific Windows
- Recall that the rectangular window transform is
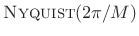 , implying the rectangular window itself is
, implying the rectangular window itself is
 ,
which is obvious.
,
which is obvious.
- The window transform for the Hamming family is
 ,
implying that Hamming windows are
,
implying that Hamming windows are
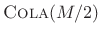 , which we also knew.
, which we also knew.
- The rectangular window transform is also
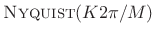 for any integer
for any integer
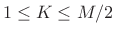 , implying that all hop sizes given
by
, implying that all hop sizes given
by 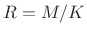 for
for
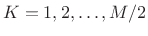 are COLA.
are COLA.
- Because its side lobes are the same width as the sinc side lobes,
the Hamming window transform is also
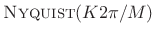 ,for any integer
,for any integer
 , implying hop sizes
, implying hop sizes 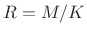 are good, for
are good, for
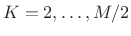 . Thus, the available hop sizes for the Hamming
window family include all of those for the rectangular window
except one (
. Thus, the available hop sizes for the Hamming
window family include all of those for the rectangular window
except one (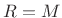 ).
).
The Nyquist Property on the Unit Circle
As a degenerate case, note that ![]() is COLA for any window, while no
window transform is
is COLA for any window, while no
window transform is
![]() except the zero window. (since it
would have to be zero at dc, and we do not consider such windows).
Did the theory break down for
except the zero window. (since it
would have to be zero at dc, and we do not consider such windows).
Did the theory break down for ![]() ?
?
Intuitively, the
![]() condition on the window transform
condition on the window transform
![]() ensures that all nonzero multiples of the
time-domain-frame-rate
ensures that all nonzero multiples of the
time-domain-frame-rate ![]() will be zeroed out over the interval
will be zeroed out over the interval
![]() along the frequency axis. When the frame-rate equals the
sampling rate (
along the frequency axis. When the frame-rate equals the
sampling rate (![]() ), there are no frame-rate multiples in the
range
), there are no frame-rate multiples in the
range
![]() . (The range
. (The range ![]() gives the same result.)
When
gives the same result.)
When ![]() , there is exactly one frame-rate multiple at
, there is exactly one frame-rate multiple at ![]() . When
. When
![]() , there are two at
, there are two at
![]() . When
. When ![]() , they are at
, they are at ![]() and
and ![]() , and so on.
, and so on.
We can cleanly handle the special case of ![]() by defining all
functions over the unit circle as being
by defining all
functions over the unit circle as being
![]() when there are no
frame-rate multiples in the range
when there are no
frame-rate multiples in the range
![]() . Thus, a discrete-time
spectrum
. Thus, a discrete-time
spectrum
![]() is said to be
is said to be
![]() if
if
![]() , for all
, for all
![]() , where
, where
![]() (the ``floor function'') denotes the greatest integer less
than or equal to
(the ``floor function'') denotes the greatest integer less
than or equal to ![]() .
.
Next Section:
Portnoff Windows
Previous Section:
Nyquist(N) Windows




















