Polyphase View of the STFT
As a familiar special case, set
| (12.66) |
where
![$\displaystyle \bold{W}_N^\ast[kn] \eqsp \left[e^{-j2\pi kn/N}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img2140.png) |
(12.67) |
The inverse of this polyphase matrix is then simply the inverse DFT matrix:
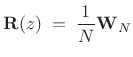 |
(12.68) |
Thus, the STFT (with rectangular window) is the simple special case of a perfect reconstruction filter bank for which the polyphase matrix is constant. It is also unitary; therefore, the STFT is an orthogonal filter bank.
The channel analysis and synthesis filters are, respectively,
![\begin{eqnarray*}
H_k(z) &=& H_0(zW_N^k)\\ [5pt]
F_k(z) &=& F_0(zW_N^{-k})
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2142.png)
where
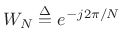 , and
, and
![$\displaystyle F_0(z)\eqsp H_0(z)\eqsp \sum_{n=0}^{N-1}z^{-n}\;\longleftrightarrow\;[1,1,\ldots,1]$](http://www.dsprelated.com/josimages_new/sasp2/img2144.png) |
(12.69) |
corresponding to the rectangular window.
Looking again at the polyphase representation of the ![]() -channel
filter bank with hop size
-channel
filter bank with hop size ![]() ,
,
![]() ,
,
![]() ,
,
![]() dividing
dividing ![]() , we have the system shown in Fig.11.25.
Following the same analysis as in §11.4.1 leads to the following
conclusion:
, we have the system shown in Fig.11.25.
Following the same analysis as in §11.4.1 leads to the following
conclusion:
Our analysis showed that the STFT using a rectangular window is
a perfect reconstruction filter bank for all
integer hop sizes in the set
![]() .
The same type of analysis can be applied to the STFT using the other
windows we've studied, including Portnoff windows.
.
The same type of analysis can be applied to the STFT using the other
windows we've studied, including Portnoff windows.
Next Section:
Example: Polyphase Analysis of the STFT with 50% Overlap, Zero-Padding, and a Non-Rectangular Window
Previous Section:
Necessary and Sufficient Conditions for Perfect Reconstruction








![\includegraphics[width=\twidth]{eps/polyNchanSTFT}](http://www.dsprelated.com/josimages_new/sasp2/img2145.png)












