DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Processing Gain

A basic property of noise signals is that they add non-coherently. This means they sum on a power basis instead of an amplitude basis. Thus, for example, if you add two separate realizations of a random process together, the total energy rises by approximately 3 dB ( $ 10\log_{10}(2)$ ). In contrast to this, sinusoids and other deterministic signals can add coherently. For example, at the midpoint between two loudspeakers putting out identical signals, a sinusoidal signal is $ 6$ dB louder than the signal out of each loudspeaker alone (cf. $ 3$ dB for uncorrelated noise).

Coherent addition of sinusoids and noncoherent addition of noise can be used to obtain any desired signal to noise ratio in a spectrum analysis of sinusoids in noise. Specifically, for each doubling of the periodogram block size in Welch's method, the signal to noise ratio (SNR) increases by 3 dB (6 dB spectral amplitude increase for all sinusoids, minus 3 dB increase for the noise spectrum).

Consider a single complex sinusoid in white noise as introduced in (5.32):

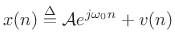$\displaystyle x(n) \isdef {\cal A}e^{j\omega_0 n} + v(n) \protect$ (7.39)

where $ {\cal A}= A e^{j\phi}$ is the complex amplitude. Then the length $ N$ DFT of the first block of $ x(n)$ is

\begin{eqnarray*} X(\omega_k) &=& \hbox{\sc DFT}_k(x) = \sum_{n=0}^{N-1}\left[{\cal A}e^{j\omega_0 n} + v(n)\right] e^{-j\omega_k n}\\ &=& {\cal A}\sum_{n=0}^{N-1}e^{j(\omega_0 -\omega_k) n} + \sum_{n=0}^{N-1}v(n) e^{-j\omega_k n}\\ &=& {\cal A}\frac{1-e^{j(\omega_0 -\omega_k)N}}{1-e^{j(\omega_0 -\omega_k)}} + V_N(\omega_k)\\ \end{eqnarray*}

For simplicity, let $ \omega_0 = \omega_l$ for some $ l$ . That is, suppose for now that $ \omega_0$ is one of the DFT frequencies $ 2\pi l/N$ , $ l=0,1,2,\ldots,N-1$ . Then

\begin{eqnarray*} X(\omega_k) &=& \left\{\begin{array}{ll} N{\cal A}+V_N(\omega_k), & k=l \\ [5pt] V_N(\omega_k), & k\neq l \\ \end{array} \right.\\ &=& N{\cal A}\delta(k-l)+V_N(\omega_k) \end{eqnarray*}

for $ k=0,1,\ldots,N-1$ . Squaring the absolute value gives

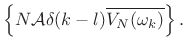$\displaystyle \left\vert X(\omega_k)\right\vert^2 = N^2 A^2\delta(k-l) + \left\vert V_N(\omega_k)\right\vert^2 + 2$re$\displaystyle \left\{N{\cal A}\delta(k-l)\overline{V_N(\omega_k)}\right\}.$ (7.40)

Since $ v(n)$ is zero mean, so is $ V(\omega_k)$ for all $ k$ . Therefore, the average over many length-$ N$ blocks will converge to

$\displaystyle {\cal E}\{\left\vert X(\omega_k)\right\vert^2\} = N^2 A^2\delta(k-l) + {\cal E}\{\left\vert V_N(\omega_k)\right\vert^2\}$ (7.41)

where $ {\cal E}\{\cdot\}$ denotes time averaging which, for stationary stochastic processes, is equivalent to taking the expected value (§C.1.6).

The final term can be expanded as

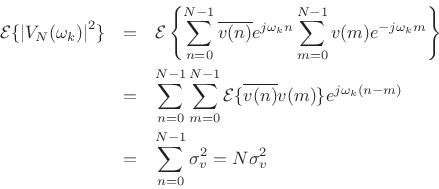
\begin{eqnarray*} {\cal E}\{\left\vert V_N(\omega_k)\right\vert^2\} &=& {\cal E}\left\{\sum_{n=0}^{N-1}\overline{v(n)} e^{j\omega_k n} \sum_{m=0}^{N-1} v(m)e^{-j\omega_k m}\right\}\\ &=& \sum_{n=0}^{N-1}\sum_{m=0}^{N-1} {\cal E}\{\overline{v(n)}v(m)\} e^{j\omega_k(n-m)}\\ &=& \sum_{n=0}^{N-1} \sigma_v^2 = N\sigma_v^2 \end{eqnarray*}

since $ {\cal E}\{\overline{v(n)}v(m)\}=\sigma_v^2\delta(n-m)$ because $ v(n)$ is white noise.

In conclusion, we have derived that the average squared-magnitude DFT of $ N$ samples of a sinusoid in white noise is given by

$\displaystyle {\cal E}\{\left\vert X(\omega_k)\right\vert^2\} = N^2 A^2\delta(k-l) + N\sigma_v^2$ (7.42)

where $ A$ is the amplitude of the complex sinusoid, and $ \sigma_v^2$ is the variance (mean square) of the noise. We see that the signal to noise ratio is zero in every bin but the $ l$ th, and in that bin it is

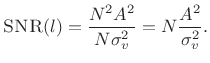$\displaystyle \hbox{\sc SNR}(l) = \frac{N^2 A^2}{N\sigma_v^2} = N\frac{A^2}{\sigma_v^2} .$ (7.43)

In the time domain, the mean square for the signal is $ A^2$ while the mean square for the noise is $ \sigma_v^2$ . Thus, the DFT gives a factor of $ N$ processing gain in the bin where the sinusoid falls. Each doubling of the DFT length adds 3 dB to the within-bin SNR. (Remember that we use $ 10\log_{10}$ for power ratios.)

Another way of viewing processing gain is to consider that the DFT performs a change of coordinates on the observations $ x$ such that all of the signal energy ``piles up'' in one coordinate $ X(\omega_l)$ , while the noise energy remains uniformly distributed among all of the coordinates.

A practical implication of the above discussion is that it is meaningless to quote signal-to-noise ratio in the frequency domain without reporting the relevant bandwidth. In the above example, the SNR could be reported as $ N A^2/\sigma_v^2$ in band $ 2\pi/N$ .

The above analysis also makes clear the effect of bandpass filtering on the signal-to-noise ratio (SNR). For example, consider a dc level $ A$ in white noise with variance $ \sigma_v^2$ . Then the SNR (mean-square level ratio) in the time domain is $ A^2/\sigma_v^2$ . Low-pass filtering at $ \omega=\pi/2$ cuts the noise energy in half but leaves the dc component unaffected, thereby increasing the SNR by $ 10\log_{10}(2)\approx 3$ dB. Each halving of the lowpass cut-off frequency adds another 3 dB to the SNR. Since the signal is a dc component (zero bandwidth), this process can be repeated indefinitely to achieve any desired SNR. The narrower the lowpass filter, the higher the SNR. Similarly, for sinusoids, the narrower the bandpass filter centered on the sinusoid's frequency, the higher the SNR.

Next Section:
The Panning Problem
Previous Section:
Filtered White Noise