Free Books    Introduction to Digital Filters  

Mass-Spring Oscillator Analysis

Consider now the mass-spring oscillator depicted physically in Fig.D.3, and in equivalent-circuit form in Fig.D.4.

Figure D.3: An ideal mass $ m$ sliding on a frictionless surface, attached via an ideal spring $ k$ to a rigid wall. The spring is at rest when the mass is centered at $ x=0$.
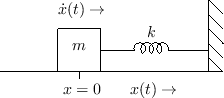\includegraphics{eps/massspringwall}

Figure D.4: Equivalent circuit for the mass-spring oscillator.
\begin{figure}\input fig/tankec.pstex_t \end{figure}

By Newton's second law of motion, the force $ f_m(t)$ applied to a mass equals its mass times its acceleration:

$\displaystyle f_m(t)=m{\ddot x}(t). $

By Hooke's law for ideal springs, the compression force $ f_k(t)$ applied to a spring is equal to the spring constant $ k$ times the displacement $ x(t)$:

$\displaystyle f_k(t)=kx(t) $

By Newton's third law of motion (``every action produces an equal and opposite reaction''), we have $ f_k = -f_m$. That is, the compression force $ f_k$ applied by the mass to the spring is equal and opposite to the accelerating force $ f_m$ exerted in the negative-$ x$ direction by the spring on the mass. In other words, the forces at the mass-spring contact-point sum to zero:

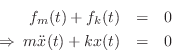
\begin{eqnarray*} f_m(t) + f_k(t) &=& 0\\ \Rightarrow\; m {\ddot x}(t) + k x(t) &=& 0 \end{eqnarray*}

We have thus derived a second-order differential equation governing the motion of the mass and spring. (Note that $ x(t)$ in Fig.D.3 is both the position of the mass and compression of the spring at time $ t$.)

Taking the Laplace transform of both sides of this differential equation gives

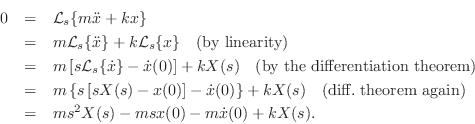
\begin{eqnarray*} 0 &=& {\cal L}_s\{m{\ddot x}+ k x\} \\ &=& m{\cal L}_s\{{\ddo... ...orem again)} \\ &=& ms^2 X(s) - msx(0) - m{\dot x}(0) + k X(s). \end{eqnarray*}

To simplify notation, denote the initial position and velocity by $ x(0)=x_0$ and $ {\dot x}(0)={\dot x}_0=v_0$, respectively. Solving for $ X(s)$ gives

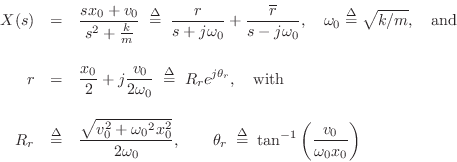
\begin{eqnarray*} X(s) &=& \frac{sx_0 + v_0}{s^2 + \frac{k}{m}} \;\isdef \; \fr... ...ta_r \;\isdef \; \tan^{-1}\left(\frac{v_0}{{\omega_0}x_0}\right) \end{eqnarray*}

denoting the modulus and angle of the pole residue $ r$, respectively. From §D.1, the inverse Laplace transform of $ 1/(s+a)$ is $ e^{-at}u(t)$, where $ u(t)$ is the Heaviside unit step function at time 0. Then by linearity, the solution for the motion of the mass is

\begin{eqnarray*} x(t) &=& re^{-j{\omega_0}t} + \overline{r}e^{j{\omega_0}t} = ... ...ga_0}t - \tan^{-1}\left(\frac{v_0}{{\omega_0}x_0}\right)\right]. \end{eqnarray*}

If the initial velocity is zero ($ v_0=0$), the above formula reduces to $ x(t) = x_0\cos({\omega_0}t)$ and the mass simply oscillates sinusoidally at frequency $ {\omega_0}= \sqrt{k/m}$, starting from its initial position $ x_0$. If instead the initial position is $ x_0=0$, we obtain

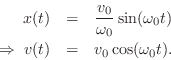
\begin{eqnarray*} x(t) &=& \frac{v_0}{{\omega_0}}\sin({\omega_0}t)\\ \;\Rightarrow\; v(t) &=& v_0\cos({\omega_0}t). \end{eqnarray*}

Mechanical Equivalent of a Capacitor is a Spring

The mechanical analog of a capacitor is the compliance of a spring. The voltage $ v(t)$ across a capacitor $ C$ corresponds to the force $ f(t)$ used to displace a spring. The charge $ q(t)$ stored in the capacitor corresponds to the displacement $ x(t)$ of the spring. Thus, Eq.$ \,$(E.2) corresponds to Hooke's law for ideal springs:

$\displaystyle x(t) = \frac{1}{k} f(t), $

where $ k$ is called the spring constant or spring stiffness. Note that Hooke's law is usually written as $ f(t) = k\,x(t)$. The quantity $ 1/k$ is called the spring compliance.

Mechanical Equivalent of an Inductor is a Mass

The mechanical analog of an inductor is a mass. The voltage $ v(t)$ across an inductor $ L$ corresponds to the force $ f(t)$ used to accelerate a mass $ m$. The current $ i(t)$ through in the inductor corresponds to the velocity $ {\dot x}(t)$ of the mass. Thus, Eq.$ \,$(E.4) corresponds to Newton's second law for an ideal mass:

$\displaystyle f(t) = m a(t), $

where $ a(t)$ denotes the acceleration of the mass $ m$.

From the defining equation $ \phi=Li$ for an inductor [Eq.$ \,$(E.3)], we see that the stored magnetic flux in an inductor is analogous to mass times velocity, or momentum. In other words, magnetic flux may be regarded as electric-charge momentum.

Next Section:
Driving Point Impedance
Previous Section:
Moving Mass