Free Books
   Free Books    Mathematics of the DFT  

Rayleigh Energy Theorem (Parseval's Theorem)


Theorem: For any $ x\in{\bf C}^N$,

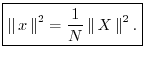
$\displaystyle \zbox {\left\Vert\,x\,\right\Vert^2 = \frac{1}{N}\left\Vert\,X\,\right\Vert^2.} $

I.e.,

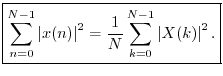
$\displaystyle \zbox {\sum_{n=0}^{N-1}\left\vert x(n)\right\vert^2 = \frac{1}{N}\sum_{k=0}^{N-1}\left\vert X(k)\right\vert^2.} $


Proof: This is a special case of the power theorem.

Note that again the relationship would be cleaner ( $ \left\Vert\,x\,\right\Vert = \vert\vert\,\tilde{X}\,\vert\vert $) if we were using the normalized DFT.

Next Section:
Stretch Theorem (Repeat Theorem)
Previous Section:
Power Theorem