Signal Metrics

This section defines some useful functions of signals (vectors).

The mean of a signal (more precisely the ``sample mean'') is defined as the average value of its samples:^5.5

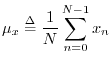
$\displaystyle \mu_x \isdef \frac{1}{N}\sum_{n=0}^{N-1}x_n$ $\displaystyle \mbox{(mean of $x$)}$

The total energy of a signal is defined as the sum of squared moduli:

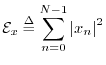
$\displaystyle {\cal E}_x \isdef \sum_{n=0}^{N-1}\left\vert x_n\right\vert^2$ $\displaystyle \mbox{(energy of $x$)}$

In physics, energy (the ``ability to do work'') and work are in units of ``force times distance,'' ``mass times velocity squared,'' or other equivalent combinations of units.^5.6 In digital signal processing, physical units are routinely discarded, and signals are renormalized whenever convenient. Therefore, ${\cal E}_x$ is defined above without regard for constant scale factors such as ``wave impedance'' or the sampling interval .

The average power of a signal is defined as the energy per sample:

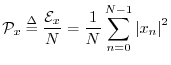
$\displaystyle {\cal P}_x \isdef \frac{{\cal E}_x}{N} = \frac{1}{N} \sum_{n=0}^{N-1}\left\vert x_n\right\vert^2$ $\displaystyle \mbox{(average power of $x$)}$

Another common description when

is real is the mean square. When

is a complex sinusoid, i.e., $x(n) = Ae^{j(\omega nT + \phi)}$ , then ${\cal P}_x = A^2$ ; in other words, for complex sinusoids, the average power equals the instantaneous power which is the amplitude squared. For real sinusoids,

re $\left\{x_n\right\}=A\cos(\omega nT+\phi)$ , we have ${\cal P}_y = A^2/2$ .

Power is always in physical units of energy per unit time. It therefore makes sense to define the average signal power as the total signal energy divided by its length. We normally work with signals which are functions of time. However, if the signal happens instead to be a function of distance (e.g., samples of displacement along a vibrating string), then the ``power'' as defined here still has the interpretation of a spatial energy density. Power, in contrast, is a temporal energy density.

The root mean square (RMS) level of a signal is simply $\sqrt{{\cal P}_x}$ . However, note that in practice (especially in audio work) an RMS level is typically computed after subtracting out any nonzero mean value.

The variance (more precisely the sample variance) of the signal is defined as the power of the signal with its mean removed:^5.7

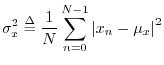
$\displaystyle \sigma_x^2 \isdef \frac{1}{N}\sum_{n=0}^{N-1}\left\vert x_n - \mu_x\right\vert^2$ $\displaystyle \mbox{(sample variance of $x$)}$

It is quick to show that, for real signals, we have

$\displaystyle \sigma_x^2 = {\cal P}_x - \mu_x^2$

which is the ``mean square minus the mean squared.'' We think of the variance as the power of the non-constant signal components (i.e., everything but dc). The terms ``sample mean'' and ``sample variance'' come from the field of statistics, particularly the theory of stochastic processes. The field of statistical signal processing [27,33,65] is firmly rooted in statistical topics such as ``probability,'' ``random variables,'' ``stochastic processes,'' and ``time series analysis.'' In this book, we will only touch lightly on a few elements of statistical signal processing in a self-contained way.

The norm (more specifically, the norm, or Euclidean norm) of a signal is defined as the square root of its total energy:

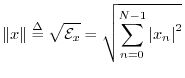
$\displaystyle \Vert x\Vert \isdef \sqrt{{\cal E}_x} = \sqrt{\sum_{n=0}^{N-1}\left\vert x_n\right\vert^2}$ $\displaystyle \mbox{(norm of $x$)}$

We think of $\Vert x\Vert$ as the length of the vector

-space. Furthermore, $\Vert x-y\Vert$ is regarded as the distance between

and

. The norm can also be thought of as the ``absolute value'' or ``radius'' of a vector.^5.8

Other Lp Norms

Since our main norm is the square root of a sum of squares,

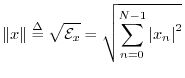
$\displaystyle \Vert x\Vert \isdef \sqrt{{\cal E}_x} = \sqrt{\sum_{n=0}^{N-1}\left\vert x_n\right\vert^2}$ $\displaystyle \mbox{(norm of $x$)}$ $\displaystyle ,$

we are using what is called an norm and we may write $\Vert x\Vert _2$ to emphasize this fact.

We could equally well have chosen a normalized norm:

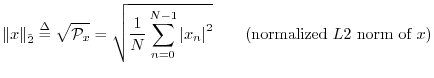
$\displaystyle \Vert x\Vert _{\tilde{2}} \isdef \sqrt{{\cal P}_x} = \sqrt{\frac{... ...N-1} \left\vert x_n\right\vert^2} \qquad \mbox{(normalized $L2$\ norm of $x$)}$

which is simply the ``RMS level'' of

(``Root Mean Square'').

More generally, the (unnormalized) norm of $x\in{\bf C}^N$ is defined as

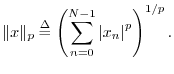
$\displaystyle \Vert x\Vert _p \isdef \left(\sum_{n=0}^{N-1}\left\vert x_n\right\vert^p\right)^{1/p}.$

(The normalized case would include

in front of the summation.) The most interesting

norms are

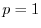: The 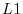, ``absolute value,'' or ``city block'' norm.
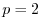: The , ``Euclidean,'' ``root energy,'' or ``least squares'' norm.
$p=\infty$ : The 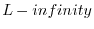, ``Chebyshev,'' ``supremum,'' ``minimax,'' or ``uniform'' norm.

Note that the case $p=\infty$ is a limiting case which becomes

$\displaystyle \Vert x\Vert _\infty = \max_{0\leq n < N} \left\vert x_n\right\vert.$

Norm Properties

There are many other possible choices of norm. To qualify as a norm on ${\bf C}^N$ , a real-valued signal-function $f(\underline{x})$ must satisfy the following three properties:

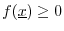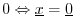
$f(\underline{x})\ge 0$ , with $0\Leftrightarrow \underline{x}=\underline{0}$
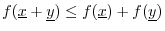
$f(\underline{x}+\underline{y})\leq f(\underline{x})+f(\underline{y})$
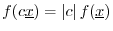$f(c\underline{x}) = \left\vert c\right\vert f(\underline{x})$ , $\forall c\in{\bf C}$

The first property, ``positivity,'' says the norm is nonnegative, and only the zero vector has norm zero. The second property is ``subadditivity'' and is sometimes called the ``triangle inequality'' for reasons that can be seen by studying Fig.5.6. The third property says the norm is ``absolutely homogeneous'' with respect to scalar multiplication. (The scalar

can be complex, in which case the angle of

has no effect).

Banach Spaces

Mathematically, what we are working with so far is called a Banach space, which is a normed linear vector space. To summarize, we defined our vectors as any list of real or complex numbers which we interpret as coordinates in the -dimensional vector space. We also defined vector addition (§5.3) and scalar multiplication (§5.5) in the obvious way. To have a linear vector space (§5.7), it must be closed under vector addition and scalar multiplication (linear combinations). I.e., given any two vectors $\underline{x}\in{\bf C}^N$ and $\underline{y}\in{\bf C}^N$ from the vector space, and given any two scalars $\alpha\in{\bf C}$ and $\beta\in{\bf C}$ from the field of scalars ${\bf C}^N$ , the linear combination $\alpha \underline{x}+ \beta\underline{y}$ must also be in the space. Since we have used the field of complex numbers ${\bf C}$ (or real numbers ${\bf R}$ ) to define both our scalars and our vector components, we have the necessary closure properties so that any linear combination of vectors from ${\bf C}^N$ lies in ${\bf C}^N$ . Finally, the definition of a norm (any norm) elevates a vector space to a Banach space.