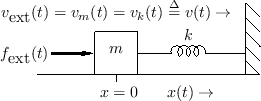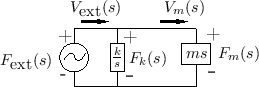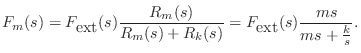DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

One-Port Network Theory

The basic idea of a one-port network [524] is shown in Fig. 7.5. The one-port is a ``black box'' with a single pair of input/output terminals, referred to as a port. A force is applied at the terminals and a velocity ``flows'' in the direction shown. The admittance ``seen'' at the port is called the driving point admittance. Network theory is normally described in terms of circuit theory elements, in which case a voltage is applied at the terminals and a current flows as shown. However, in our context, mechanical elements are preferable.

Figure 7.5: A one-port network characterized by its driving point admittance $ \Gamma (s)$. For any applied force $ F(s)$, the observed velocity is $ V(s) = \Gamma (s)F(s)$.
\includegraphics[scale=0.9]{eps/loneport}

Series Combination of One-Ports

Figure 7.6 shows the series combination of two one-ports.

Figure 7.6: Two one-port networks combined in series. The impedance of the series combination is $ R(s) = F(s)/V(s) = R_1(s) + R_2(s)$.
\includegraphics[scale=0.9]{eps/lseries}

Impedances add in series, so the aggregate impedance is $ R(s) = R_1(s) + R_2(s)$, and the admittance is

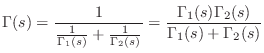
$\displaystyle \Gamma(s) = \frac{1}{\frac{1}{\Gamma_1(s)} + \frac{1}{\Gamma_2(s)}} = \frac{\Gamma_1(s) \Gamma_2(s) }{\Gamma_1(s) + \Gamma_2(s)} $

The latter expression is the handy product-over-sum rule for combining admittances in series.

Mass-Spring-Wall System

In a physical situation, if two elements are connected in such a way that they share a common velocity, then they are in series. An example is a mass connected to one end of a spring, where the other end is attached to a rigid support, and the force is applied to the mass, as shown in Fig. 7.7.

Figure 7.7: A mass and spring combined as one-ports in series.
\includegraphics{eps/lseriesExample}

Figure 7.8 shows the electrical equivalent circuit corresponding to Fig.7.7.

Figure: Electrical equivalent circuit of the series mass-spring driven by an external force diagrammed in Fig.7.7.
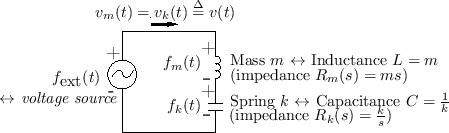\includegraphics{eps/lseriesec}

Figure: Impedance diagram for the force-driven, series arrangement of mass and spring shown in Fig.7.7.
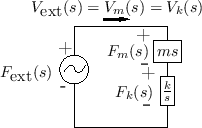\includegraphics{eps/lseriesid}

Parallel Combination of One-Ports

Figure Fig.7.10 shows the parallel combination of two one-ports.

Figure 7.10: Two one-port networks combined in parallel. The admittance of the parallel combination is $ \Gamma (s) = \Gamma _1(s) + \Gamma _2(s)$.
\includegraphics[scale=0.9]{eps/lparallel}

Admittances add in parallel, so the combined admittance is $ \Gamma (s) = \Gamma _1(s) + \Gamma _2(s)$, and the impedance is

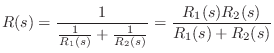
$\displaystyle R(s) = \frac{1}{\frac{1}{R_1(s)} + \frac{1}{R_2(s)}} = \frac{R_1(s) R_2(s) }{R_1(s) + R_2(s)} $

which is the familiar product-over-sum rule for combining impedances in parallel. This operation is often denoted by

$\displaystyle R= R_1 \vert\vert R_2 $

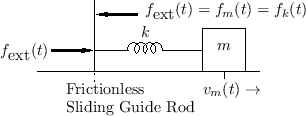
Spring-Mass System

When two physical elements are driven by a common force (yet have independent velocities, as we'll soon see is quite possible), they are formally in parallel. An example is a mass connected to a spring in which the driving force is applied to one end of the spring, and the mass is attached to the other end, as shown in Fig.7.11. The compression force on the spring is equal at all times to the rightward force on the mass. However, the spring compression velocity $ v_k(t)$ does not always equal the mass velocity $ v_m(t)$. We do have that the sum of the mass velocity and spring compression velocity gives the velocity of the driving point, i.e., $ v(t)=v_m(t)+v_k(t)$. Thus, in a parallel connection, forces are equal and velocities sum.

Figure 7.11: A mass and spring combined as one-ports in parallel.
\includegraphics{eps/lparallelExample}

Figure 7.12 shows the electrical equivalent circuit corresponding to Fig.7.11.

Figure: Electrical equivalent circuit of the parallel mass-spring combination driven by an external force, as diagrammed in Fig.7.11.
\includegraphics{eps/lparallelec}

Figure: Impedance diagram for the force-driven, parallel mass-spring arrangement shown in Fig.7.11.
\includegraphics{eps/lparallelid}

Mechanical Impedance Analysis

Impedance analysis is commonly used to analyze electrical circuits [110]. By means of equivalent circuits, we can use the same analysis methods for mechanical systems.

For example, referring to Fig.7.9, the Laplace transform of the force on the spring $ k$ is given by the so-called voltage divider relation:8.2

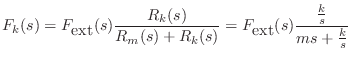
$\displaystyle F_k(s) = F_{\mbox{ext}}(s) \frac{R_k(s)}{R_m(s)+R_k(s)} = F_{\mbox{ext}}(s) \frac{\frac{k}{s}}{ms+\frac{k}{s}} $

Similarly, the Laplace transform of the force on the mass $ m$ is given by

$\displaystyle F_m(s) = F_{\mbox{ext}}(s) \frac{R_m(s)}{R_m(s)+R_k(s)} = F_{\mbox{ext}}(s) \frac{ms}{ms+\frac{k}{s}}. \protect$ (8.1)

As a simple application, let's find the motion of the mass $ m$, after time zero, given that the input force is an impulse at time 0:

$\displaystyle f_{\mbox{ext}}(t)=\delta(t) \;\leftrightarrow\; F_{\mbox{ext}}(s)=1 $

Then, by the ``voltage divider'' relation Eq.$ \,$(7.1), the Laplace transform of the mass force $ f_m(t)$ after time 0 is given by

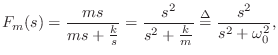
$\displaystyle F_m(s) = \frac{ms}{ms+\frac{k}{s}} = \frac{s^2}{s^2+\frac{k}{m}} \isdef \frac{s^2}{s^2+\omega_0^2}, $

where we have defined $ \omega_0^2\isdef k/m$. The mass velocity Laplace transform is then

\begin{eqnarray*} V_m(s) &=& \frac{F_m(s)}{ms} \;=\; \frac{1}{m} \cdot \frac{s}{... ...}\right]\\ [5pt] &\leftrightarrow& \frac{1}{m} \cos(\omega_0 t). \end{eqnarray*}

Thus, the impulse response of the mass oscillates sinusoidally with radian frequency $ \omega_0=\sqrt{k/m}$, and amplitude $ 1/m$. The velocity starts out maximum at time $ t=0$, which makes physical sense. Also, the momentum transferred to the mass at time 0 is $ m\,v(0+) = 1$; this is also expected physically because the time-integral of the applied force is 1 (the area under any impulse $ \delta(t)$ is 1).

General One-Ports

An arbitrary interconnection of $ N$ impedances and admittances, with input and output force and/or velocities defined, results in a one-port with admittance expressible as

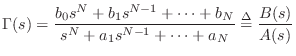
$\displaystyle \Gamma(s) = \frac{b_0 s^N + b_1 s^{N-1} + \cdots + b_N}{s^N + a_1 s^{N-1} + \cdots + a_N} \isdef \frac{B(s)}{A(s)} $

In any mechanical situation we have $ b_0 = 0$, in principle, since at sufficiently high frequencies, every mechanical system must ``look like a mass.''8.3 However, for purposes of approximation to a real physical system, it may well be best to allow $ b_0\neq 0$ and consider the above expression to be a rational approximation to the true admittance function.

Passive One-Ports

It is well known that the impedance of every passive one-port is positive real (see §C.11.2). The reciprocal of a positive real function is positive real, so every passive impedance corresponds also to a passive admittance.

A complex-valued function of a complex variable $ \Gamma (s)$ is said to be positive real (PR) if

1)
$ \Gamma (s)$ is real whenever $ s$ is real
2)
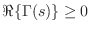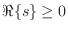$ \Re\{\Gamma(s)\} \geq 0$ whenever $ \Re\{s\} \geq 0$.

A particularly important property of positive real functions is that the phase is bounded between plus and minus $ 90$ degrees, i.e.,

$\displaystyle -\frac{\pi}{2} \leq \angle{\Gamma(j\omega)} \leq \frac{\pi}{2} $

This is a significant constraint on the rational function $ \Gamma (s)$. One implication is that in the lossless case (no dashpots, only masses and springs--a reactance) all poles and zeros interlace along the $ j\omega $ axis, as depicted in Fig.7.14.

Figure 7.14: Poles and zeros of a lossless immittance (reactance or suseptance) must interlace along the $ j\omega $ Axis. Left: Pole-zero plot. Right: Phase response. The ``spring/mass'' labels along the frequency axis correspond to the case of a lossless admittance (susceptance) in which a spring admittance ( $ \Gamma _k(j\omega )=j\omega /k$) gives a $ +\pi /2$ phase shift, while that of a mass ( $ \Gamma _m(j\omega )=-j/(m\omega )$) gives a $ -\pi /2$ phase shift between the input driving-force and output velocity.
\includegraphics[width=\twidth]{eps/interlace}

Referring to Fig.7.14, consider the graphical method for computing phase response of a reactance from the pole zero diagram [449].8.4Each zero on the positive $ j\omega $ axis contributes a net 90 degrees of phase at frequencies above the zero. As frequency crosses the zero going up, there is a switch from $ -90$ to $ +90$ degrees. For each pole, the phase contribution switches from $ +90$ to $ -90$ degrees as it is passed going up in frequency. In order to keep phase in $ [-\pi/2,\pi/2]$, it is clear that the poles and zeros must strictly alternate. Moreover, all poles and zeros must be simple, since a multiple poles or zero would swing the phase by more than $ 180$ degrees, and the reactance could not be positive real.

The positive real property is fundamental to passive immittances and comes up often in the study of measured resonant systems. A practical modeling example (passive digital modeling of a guitar bridge) is discussed in §9.2.1.

Next Section:
Digitization of Lumped Models
Previous Section:
Impedance