DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Rigid Terminations

A rigid termination is the simplest case of a string (or tube) termination. It imposes the constraint that the string (or air) cannot move at the termination. (We'll look at the more practical case of a yielding termination in §9.2.1.) If we terminate a length $ L$ ideal string at $ x=0$ and $ x=L$, we then have the ``boundary conditions''

$\displaystyle y(t,0) \equiv 0 \qquad y(t,L) \equiv 0 \protect$ (7.9)

where ``$ \equiv$'' means ``identically equal to,'' i.e., equal for all $ t$. Let $ N\isdef 2L/X$ denote the time in samples to propagate from one end of the string to the other and back, or the total ``string loop'' delay. The loop delay $ N$ is also equal to twice the number of spatial samples along the string.

Applying the traveling-wave decomposition from Eq.$ \,$(6.2), we have

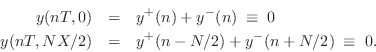
\begin{eqnarray*} y(nT,0) &=& y^{+}(n) + y^{-}(n) \;\equiv\; 0\\ y(nT,NX/2) &=& y^{+}(n-N/2) + y^{-}(n+N/2) \;\equiv\; 0. \end{eqnarray*}

Therefore, solving for the reflected waves gives

$\displaystyle y^{+}(n)$ $\displaystyle =$ $\displaystyle -y^{-}(n)$ (7.10)
$\displaystyle y^{-}(n+N/2)$ $\displaystyle =$ $\displaystyle -y^{+}(n-N/2).$ (7.11)

A digital simulation diagram for the rigidly terminated ideal string is shown in Fig.6.3. A ``virtual pickup'' is shown at the arbitrary location $ x=\xi $.

Figure 6.3: The rigidly terminated ideal string, with a displacement output indicated at position $ x=\xi $. Rigid terminations reflect traveling displacement, velocity, or acceleration waves with a sign inversion. Slope or force waves reflect with no sign inversion.
\includegraphics[width=\twidth]{eps/fterminatedstring}

Velocity Waves at a Rigid Termination

Since the displacement is always zero at a rigid termination, the velocity is also zero there:

$\displaystyle v(t,0) \equiv 0 \qquad v(t,L) \equiv 0 $

Therefore, velocity waves reflect from a rigid termination with a sign flip, just like displacement waves:
$\displaystyle v^{+}(n)$ $\displaystyle =$ $\displaystyle -v^{-}(n)$  
$\displaystyle v^{-}(n+N/2)$ $\displaystyle =$ $\displaystyle -v^{+}(n-N/2) \protect$ (7.12)

Such inverting reflections for velocity waves at a rigid termination are identical for models of vibrating strings and acoustic tubes.

Force or Pressure Waves at a Rigid Termination

To find out how force or pressure waves recoil from a rigid termination, we may convert velocity waves to force or velocity waves by means of the Ohm's law relations of Eq.$ \,$(6.6) for strings (or Eq.$ \,$(6.7) for acoustic tubes), and then use Eq.$ \,$(6.12), and then Eq.$ \,$(6.6) again:

\begin{eqnarray*} f^{{+}}(n) &=&Rv^{+}(n) \eqsp -Rv^{-}(n) \eqsp f^{{-}}(n) \\ ... ...+N/2) &=&-Rv^{-}(n+N/2) \eqsp Rv^{+}(n-N/2) \eqsp f^{{+}}(n-N/2) \end{eqnarray*}

Thus, force (and pressure) waves reflect from a rigid termination with no sign inversion:7.3

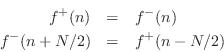
\begin{eqnarray*} f^{{+}}(n) &=& f^{{-}}(n) \\ f^{{-}}(n+N/2) &=& f^{{+}}(n-N/2) \end{eqnarray*}

The reflections from a rigid termination in a digital-waveguide acoustic-tube simulation are exactly analogous:

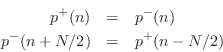
\begin{eqnarray*} p^+(n) &=& p^-(n) \\ p^-(n+N/2) &=& p^+(n-N/2) \end{eqnarray*}

Waveguide terminations in acoustic stringed and wind instruments are never perfectly rigid. However, they are typically passive, which means that waves at each frequency see a reflection coefficient not exceeding 1 in magnitude. Aspects of passive ``yielding'' terminations are discussed in §C.11.

Next Section:
Moving Rigid Termination
Previous Section:
Ideal Acoustic Tube