Convolution of Short Signals
Figure 8.1 illustrates the conceptual operation of filtering an input
signal ![]() by a filter with impulse-response
by a filter with impulse-response ![]() to produce an
output signal
to produce an
output signal ![]() . By the convolution theorem for DTFTs
(§2.3.5),
. By the convolution theorem for DTFTs
(§2.3.5),
| (9.9) |
or,
| (9.10) |
where
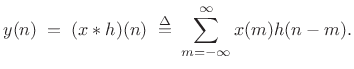 |
(9.11) |
In practice, we always use the DFT (preferably an FFT) in place of the DTFT, in which case we may write
| (9.12) |
where now
where
Another way to look at convolution is as the inner product of ![]() , and
, and
![]() , where
, where
![]() , i.e.,
, i.e.,
| (9.14) |
This form describes graphical convolution in which the output sample at time
Cyclic FFT Convolution
Thanks to the convolution theorem, we have two alternate ways to perform cyclic convolution in practice:
- Direct calculation in the time domain using (8.13)
- Frequency-domain convolution:
- Fourier Transform both signals
- Perform term by term multiplication of the transformed signals
- Inverse transform the result to get back to the time domain
Acyclic FFT Convolution
If we add enough trailing zeros to the signals being convolved, we can
obtain acyclic convolution embedded within a cyclic
convolution. How many zeros do we need to add? Suppose the signal
![]() consists of
consists of ![]() contiguous nonzero samples at times 0
to
contiguous nonzero samples at times 0
to
![]() , preceded and followed by zeros, and suppose
, preceded and followed by zeros, and suppose ![]() is nonzero
only over a block of
is nonzero
only over a block of ![]() samples starting at time 0. Then the
acyclic convolution of
samples starting at time 0. Then the
acyclic convolution of ![]() with
with ![]() reduces to
reduces to
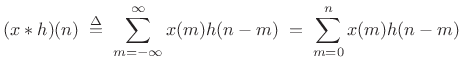 |
(9.15) |
which is zero for
The number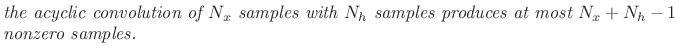
| (9.16) |
and so on.
When ![]() or
or ![]() is infinity, the convolution result can be as
small as 1. For example, consider
is infinity, the convolution result can be as
small as 1. For example, consider
![]() , with
, with
![]() , and
, and
![]() . Then
. Then
![]() . This is an example of what is called deconvolution.
In the frequency domain, deconvolution always involves a pole-zero
cancellation. Therefore, it is only possible when
. This is an example of what is called deconvolution.
In the frequency domain, deconvolution always involves a pole-zero
cancellation. Therefore, it is only possible when ![]() or
or ![]() is
infinite. In practice, deconvolution can sometimes be accomplished
approximately, particularly within narrow frequency bands
[119].
is
infinite. In practice, deconvolution can sometimes be accomplished
approximately, particularly within narrow frequency bands
[119].
We thus conclude that, to embed acyclic convolution within a cyclic
convolution (as provided by an FFT), we need to zero-pad both
operands out to length ![]() , where
, where ![]() is at least the sum of the
operand lengths (minus one).
is at least the sum of the
operand lengths (minus one).
Acyclic Convolution in Matlab
In Matlab or Octave, the conv function implements acyclic convolution:
octave:1> conv([1 2],[3 4]) ans = 3 10 8Note that it returns an output vector which is long enough to accommodate the entire result of the convolution, unlike the filter primitive, which always returns an output signal equal in length to the input signal:
octave:2> filter([1 2],1,[3 4]) ans = 3 10 octave:3> filter([1 2],1,[3 4 0]) ans = 3 10 8
Pictorial View of Acyclic Convolution
Figure 8.2 shows schematically the result of convolving
two zero-padded signals ![]() and
and ![]() . In this case, the signal
. In this case, the signal ![]() starts some time after
starts some time after ![]() , say at
, say at ![]() . Since
. Since ![]() begins at
time 0
, the output starts promptly at time
begins at
time 0
, the output starts promptly at time ![]() , but it takes some
time to ``ramp up'' to full amplitude. (This is the transient
response of the FIR filter
, but it takes some
time to ``ramp up'' to full amplitude. (This is the transient
response of the FIR filter ![]() .) If the length of
.) If the length of ![]() is
is ![]() , then
the transient response is finished at time
, then
the transient response is finished at time
![]() . Next, when
the input signal goes to zero at time
. Next, when
the input signal goes to zero at time ![]() , the output reaches
zero
, the output reaches
zero ![]() samples later (after the filter ``decay time''), or time
samples later (after the filter ``decay time''), or time
![]() . Thus, the total number of nonzero output samples is
. Thus, the total number of nonzero output samples is
![]() .
.
If we don't add enough zeros, some of our convolution terms ``wrap around'' and add back upon others (due to modulo indexing). This can be called time-domain aliasing. Zero-padding in the time domain results in more samples (closer spacing) in the frequency domain, i.e., a higher `sampling rate' in the frequency domain. If we have a high enough spectral sampling rate, we can avoid time aliasing.
The motivation for implementing acyclic convolution using a
zero-padded cyclic convolution is that we can use a Cooley-Tukey Fast Fourier
Transform (FFT) to implement cyclic convolution when its length ![]() is
a power of 2.
is
a power of 2.
Acyclic FFT Convolution in Matlab
The following example illustrates the implementation of acyclic convolution using a Cooley-Tukey FFT in matlab:
x = [1 2 3 4]; h = [1 1 1]; nx = length(x); nh = length(h); nfft = 2^nextpow2(nx+nh-1) xzp = [x, zeros(1,nfft-nx)]; hzp = [h, zeros(1,nfft-nh)]; X = fft(xzp); H = fft(hzp); Y = H .* X; format bank; y = real(ifft(Y)) % zero-padded result yt = y(1:nx+nh-1) % trim and print yc = conv(x,h) % for comparisonProgram output:
nfft = 8
y =
1.00 3.00 6.00 9.00 7.00 4.00 0.00 0.00
yt =
1.00 3.00 6.00 9.00 7.00 4.00
yc =
1 3 6 9 7 4
FFT versus Direct Convolution
Using the Matlab test program in
[264],9.1FFT convolution was found to be faster than direct convolution
starting at length ![]() (looking only at powers of 2 for the
length
(looking only at powers of 2 for the
length ![]() ).9.2 FFT convolution was also never
significantly slower at shorter lengths for which ``calling overhead''
dominates.
).9.2 FFT convolution was also never
significantly slower at shorter lengths for which ``calling overhead''
dominates.
Running the same test program in 2011,9.3 FFT convolution using the
fft function was found to be faster than conv for
all (power-of-2) lengths. The speed of FFT convolution divided
by that of direct convolution started out at 14 for ![]() , fell to a
minimum of
, fell to a
minimum of ![]() at
at ![]() , above which it started to climb as
expected, reaching
, above which it started to climb as
expected, reaching ![]() at
at
![]() . Note that this
comparison is unfair because the Octave fft function is a
dynamically linked, separately compiled module, while conv is
written in the matlab language and thus suffers more overhead from the
matlab interpreter.
. Note that this
comparison is unfair because the Octave fft function is a
dynamically linked, separately compiled module, while conv is
written in the matlab language and thus suffers more overhead from the
matlab interpreter.
An analysis reported in Strum and Kirk [279, p. 521],
based on the number of real multiplies, predicts that the fft
is faster starting at length ![]() , and that direct convolution is
significantly faster for very short convolutions (e.g., 16 operations
for a direct length-4 convolution, versus 176 for the fft
function).
, and that direct convolution is
significantly faster for very short convolutions (e.g., 16 operations
for a direct length-4 convolution, versus 176 for the fft
function).
See [264]9.4for further discussion of FFT algorithms and their applications.
In digital audio, FIR filters are often hundreds of taps long. For
such filters, the FFT method is much faster than direct convolution in
the time domain on single CPUs. On GPUs, FFT convolution is faster
than direct convolution only for much longer FIR-filter lengths (in
the thousands of taps [242]); this is because
massively parallel hardware can perform an
![]() algorithm
(direct convolution) faster than a single CPU can perform an
algorithm
(direct convolution) faster than a single CPU can perform an
![]() algorithm (FFT convolution).
algorithm (FFT convolution).
Audio FIR Filters
FIR filters shorter than the ear's ``integration time'' can generally be characterized by their magnitude frequency response (no perceivable ``delay effects''). The nominal ``integration time'' of the ear can be defined as the reciprocal of a critical bandwidth of hearing. Using Zwicker's definition of critical bandwidth [305], the smallest critical bandwidth of hearing is approximately 100 Hz (below 500 Hz). Thus, the nominal integration time of the ear is 10ms below 500 Hz. (Using the equivalent-rectangular-bandwidth (ERB) definition of critical bandwidth [179,269], longer values are obtained). At a 50 kHz sampling rate, this is 500 samples. Therefore, FIR filters shorter than the ear's ``integration time,'' i.e., perceptually ``instantaneous,'' can easily be hundreds of taps long (as discussed in the next section). FFT convolution is consequently an important implementation tool for FIR filters in digital audio applications.
Example 1: Low-Pass Filtering by FFT Convolution
In this example, we design and implement a length ![]() FIR lowpass
filter having a cut-off frequency at
FIR lowpass
filter having a cut-off frequency at ![]() Hz. The filter is
tested on an input signal
Hz. The filter is
tested on an input signal ![]() consisting of a sum of sinusoidal
components at frequencies
consisting of a sum of sinusoidal
components at frequencies
![]() Hz. We'll filter a
single input frame of length
Hz. We'll filter a
single input frame of length ![]() , which allows the FFT to be
, which allows the FFT to be
![]() samples (no wasted zero-padding).
samples (no wasted zero-padding).
% Signal parameters: f = [ 440 880 1000 2000 ]; % frequencies M = 256; % signal length Fs = 5000; % sampling rate % Generate a signal by adding up sinusoids: x = zeros(1,M); % pre-allocate 'accumulator' n = 0:(M-1); % discrete-time grid for fk = f; x = x + sin(2*pi*n*fk/Fs); end
Next we design the lowpass filter using the window method:
% Filter parameters: L = 257; % filter length fc = 600; % cutoff frequency % Design the filter using the window method: hsupp = (-(L-1)/2:(L-1)/2); hideal = (2*fc/Fs)*sinc(2*fc*hsupp/Fs); h = hamming(L)' .* hideal; % h is our filter
Figure 8.3 plots the impulse response and amplitude response of our FIR filter designed by the window method. Next, the signal frame and filter impulse response are zero-padded out to the FFT size and transformed:
% Choose the next power of 2 greater than L+M-1 Nfft = 2^(ceil(log2(L+M-1))); % or 2^nextpow2(L+M-1) % Zero pad the signal and impulse response: xzp = [ x zeros(1,Nfft-M) ]; hzp = [ h zeros(1,Nfft-L) ]; X = fft(xzp); % signal H = fft(hzp); % filter
Figure 8.4 shows the input signal spectrum and the filter amplitude response overlaid. We see that only one sinusoidal component falls within the pass-band.
![\includegraphics[width=\twidth,height=1.8in]{eps/filtered_transform}](http://www.dsprelated.com/josimages_new/sasp2/img1367.png) |
Now we perform cyclic convolution in the time domain using pointwise multiplication in the frequency domain:
Y = X .* H;The modified spectrum is shown in Fig.8.5.
The final acyclic convolution is the inverse transform of the pointwise product in the frequency domain. The imaginary part is not quite zero as it should be due to finite numerical precision:
y = ifft(Y); relrmserr = norm(imag(y))/norm(y) % check... should be zero y = real(y);
![\includegraphics[width=\twidth]{eps/filteredSignalAnn}](http://www.dsprelated.com/josimages_new/sasp2/img1368.png) |
Figure 8.6 shows the filter output signal in the time domain. As expected, it looks like a pure tone in steady state. Note the equal amounts of ``pre-ringing'' and ``post-ringing'' due to the use of a linear-phase FIR filter.9.5
For an input signal approximately ![]() samples long, this example is
2-3 times faster than the conv function in Matlab (which is
precompiled C code implementing time-domain convolution).
samples long, this example is
2-3 times faster than the conv function in Matlab (which is
precompiled C code implementing time-domain convolution).
Example 2: Time Domain Aliasing
Figure 8.7 shows the effect of insufficient zero padding, which can be thought of as undersampling in the frequency domain. We will see aliasing in the time domain results.
The lowpass filter length is ![]() and the input signal consists of
an impulse at times
and the input signal consists of
an impulse at times ![]() and
and
![]() , where the data frame
length is
, where the data frame
length is ![]() . To avoid time aliasing (i.e., to implement
acyclic convolution using an FFT), we must use an FFT size
. To avoid time aliasing (i.e., to implement
acyclic convolution using an FFT), we must use an FFT size ![]() at
least as large as
at
least as large as
![]() . In the figure, the FFT sizes
. In the figure, the FFT sizes ![]() ,
,
![]() , and
, and ![]() are used. Thus, the first case is heavily time
aliased, the second only slightly time aliased (involving only some of
the filter's ``ringing'' after the second pulse), and the third is
free of time aliasing altogether.
are used. Thus, the first case is heavily time
aliased, the second only slightly time aliased (involving only some of
the filter's ``ringing'' after the second pulse), and the third is
free of time aliasing altogether.
![\includegraphics[width=\twidth]{eps/badoverlap}](http://www.dsprelated.com/josimages_new/sasp2/img1378.png) |
Next Section:
Convolving with Long Signals
Previous Section:
Summary








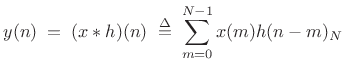
![\includegraphics[width=\textwidth ]{eps/convwaves}](http://www.dsprelated.com/josimages_new/sasp2/img1344.png)
![\includegraphics[width=\twidth]{eps/filter}](http://www.dsprelated.com/josimages_new/sasp2/img1365.png)
![\includegraphics[width=\twidth,height=1.8in]{eps/signal_transform}](http://www.dsprelated.com/josimages_new/sasp2/img1366.png)












