Free Books    Spectral Audio Signal Processing  

Filter-Bank Summation (FBS) Interpretation of the STFT

We can group the terms in the STFT definition differently to obtain the filter-bank interpretation:

$\displaystyle X_m(\omega_k)$ $\displaystyle =$ $\displaystyle \sum_{n=-\infty}^\infty \underbrace{[ x(n)e^{-j\omega_k n}]}_{x_k(n)} w(n-m)$  
  $\displaystyle =$ $\displaystyle \left[x_k \ast \hbox{\sc Flip}(w)\right](m) \protect$ (10.2)

As will be explained further below (and illustrated further in Figures 9.3, 9.4, and 9.5), under the filter-bank interpretation, the spectrum of $ x$ is first rotated along the unit circle in the $ z$ plane so as to shift frequency $ \omega_k$ down to 0 (via modulation by $ e^{-j\omega_k n}$ in the time domain), thus forming the heterodyned signal $ x_k(n)\isdeftext x(n)\exp(-j\omega_k n)$ . Next, the heterodyned signal $ x_k(n)$ is lowpass-filtered to a narrow band about frequency 0 (via convolving with the time-reversed window $ \hbox{\sc Flip}(w)$ ). The STFT is thus interpreted as a frequency-ordered collection of narrow-band time-domain signals, as depicted in Fig.9.2. In other words, the STFT can be seen as a uniform filter bank in which the input signal $ x(n)$ is converted to a set of $ N$ time-domain output signals $ X_n(\omega_k)$ , $ k=0,1,\ldots,N-1$ , one for each channel of the $ N$ -channel filter bank.

Figure 9.2: Filter Bank Summation (FBS) view of the STFT
\includegraphics{eps/fbs}

Expanding on the previous paragraph, the STFT (9.2) is computed by the following operations:

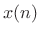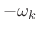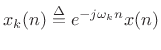  • Frequency-shift $ x(n)$ by $ -\omega_k$ to get $ x_k(n) \mathrel{\stackrel{\Delta}{=}}e^{-j\omega_k n}x(n)$ .
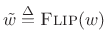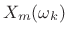  • Convolve $ x_k(n)$ with $ {\tilde w}\mathrel{\stackrel{\Delta}{=}}\hbox{\sc Flip}(w)$ to get $ X_m(\omega_k)$ :

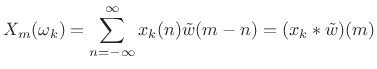
    $\displaystyle X_m(\omega_k) = \sum_{n=-\infty}^\infty x_k(n){\tilde w}(m-n) = (x_k * {\tilde w})(m)$ (10.3)

The STFT output signal $ X_m(\omega_k)$ is regarded as a time-domain signal (time index $ m$ ) coming out of the $ k$ th channel of an $ N$ -channel filter bank. The center frequency of the $ k$ th channel filter is $ \omega_k = 2\pi k/N$ , $ k=0,1,\ldots,N-1$ . Each channel output signal is a baseband signal; that is, it is centered about dc, with the ``carrier term'' $ e^{j\omega_k m}$ taken out by ``demodulation'' (frequency-shifting). In particular, the $ k$ th channel signal is constant whenever the input signal happens to be a sinusoid tuned to frequency $ \omega_k$ exactly.

Note that the STFT analysis window $ w$ is now interpreted as (the flip of) a lowpass-filter impulse response. Since the analysis window $ w$ in the STFT is typically symmetric, we usually have $ \hbox{\sc Flip}(w)=w$ . This filter is effectively frequency-shifted to provide each channel bandpass filter. If the cut-off frequency of the window transform is $ \omega_c$ (typically half a main-lobe width), then each channel signal can be downsampled significantly. This downsampling factor is the FBS counterpart of the hop size $ R$ in the OLA context.

Figure 9.3 illustrates the filter-bank interpretation for $ R=1$ (the ``sliding STFT''). The input signal $ x(n)$ is frequency-shifted by a different amount for each channel and lowpass filtered by the (flipped) window.

\begin{psfrags} % latex2html id marker 23871\psfrag{w}{\Large$\protect\hbox{\sc Flip}(w)$}\psfrag{x(n)}{\LARGE$x(n)$}\psfrag{X0}{\LARGE$X_n(\omega_{\scriptscriptstyle 0}$)}\psfrag{X1}{\LARGE$X_n(\omega_{\scriptscriptstyle 1}$)}\psfrag{XNm1}{\LARGE$X_n(\omega_{\scriptscriptstyle {N}-1})$}\psfrag{ejw0}{\huge$e^{-j\omega_{\scriptscriptstyle 0}n}$}\psfrag{ejw1}{\huge$e^{-j\omega_{\scriptscriptstyle 1}n}$}\psfrag{ejwNm1}{\huge$e^{-j\omega_{\scriptscriptstyle {N-1}}n}$}\psfrag{dR}{\LARGE$\downarrow R$}\psfrag{X}{\LARGE$\times$}\begin{figure}[htbp] \includegraphics[width=3in]{eps/fbs1} \caption{Sliding STFT analysis filter bank. The $k$th channel of the filter bank computes $X_n(\omega_k)=(x_k\ast \hbox{\sc Flip}{w})(n)$, where $x_k(n)\isdeftext x(n)\exp(-j\omega_k n)$. } \end{figure} \end{psfrags}

Next Section:
FBS and Perfect Reconstruction
Previous Section:
Overlap-Add (OLA) Interpretation of the STFT