Filtered White Noise

Free Books Spectral Audio Signal Processing

When a white-noise sequence is filtered, successive samples generally become correlated.^7.8 Some of these filtered-white-noise signals have names:

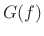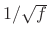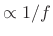pink noise: Filter amplitude response is proportional to $1/\sqrt{f}$ ; PSD $\propto 1/f$ (``1/f noise'' -- ``equal-loudness noise'')
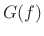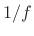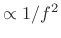brown noise: Filter amplitude response is proportional to ; PSD $\propto 1/f^2$ (``Brownian motion'' -- ``Wiener process'' -- ``random increments'')

More generally, filtered white noise can be termed colored noise or correlated noise. As long as the filter is linear and time-invariant (LTI), and strictly stable (poles inside and not on the unit circle of the plane), its output will be a stationary ``colored noise''. We will only consider stochastic processes of this nature.

In the preceding sections, we have looked at two ways of analyzing noise: the sample autocorrelation function in the time or ``lag'' domain, and the sample power spectral density (PSD) in the frequency domain. We now look at these two representations for the case of filtered noise.

Let denote a length sequence we wish to analyze. Then the Bartlett-windowed acyclic sample autocorrelation of is $x\star x$ , and the corresponding smoothed sample PSD is $\left\vert X(\omega)\right\vert^2$ (§6.7, §2.3.6).

For filtered white noise, we can write as a convolution of white noise and some impulse response :

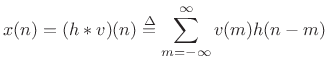$\displaystyle x(n) = (h\ast v)(n) \isdef \sum_{m=-\infty}^\infty v(m)h(n-m)$

(7.29)

The DTFT of is then, by the convolution theorem (§2.3.5),

$\displaystyle X(\omega) = H(\omega)V(\omega)$

(7.30)

so that

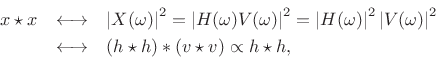
$\begin{eqnarray*} x\star x &\longleftrightarrow& \left\vert X(\omega)\right\vert^2 = \left\vert H(\omega)V(\omega)\right\vert^2 = \left\vert H(\omega)\right\vert^2\left\vert V(\omega)\right\vert^2\\ &\longleftrightarrow& (h\star h)\ast (v\star v) \propto h\star h, \end{eqnarray*}$

since $v\star v \propto \sigma_v^2\delta$ for white noise. Thus, we have derived that the autocorrelation of filtered white noise is proportional to the autocorrelation of the impulse response times the variance of the driving white noise.

Let's try to pin this down more precisely and find the proportionality constant. As the number of observed samples of $x(n) = (h\ast v)(n)$ goes to infinity, the length- Bartlett-window bias $M-\vert l\vert$ in the autocorrelation $x\star x$ converges to a constant scale factor at lags such that $M\gg \vert l\vert$ . Therefore, the unbiased autocorrelation can be expressed as

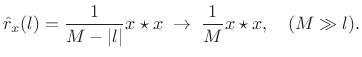$\displaystyle \hat{r}_x(l) = \frac{1}{M-\vert l\vert} x\star x \;\to\; \frac{1}{M} x \star x, \quad \hbox{($M\gg l$)}.$

(7.31)

In the limit, we obtain

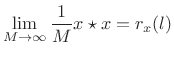$\displaystyle \lim_{M\to\infty} \frac{1}{M} x \star x = r_x(l)$

(7.32)

In the frequency domain we therefore have

$\begin{eqnarray*} S_x(\omega) &=& \lim_{M\to \infty}\frac{1}{M}\vert X(\omega)\vert^2 \;=\; % = \frac{1}{M}\vert H(\omega)\,V(\omega)\vert^2 \vert H(\omega)\vert^2 \cdot \lim_{M\to \infty} \frac{\vert V(\omega)\vert^2}{M} \\ [5pt] &=& \vert H(\omega)\vert^2 S_v(\omega) \;=\; \vert H(\omega)\vert^2\sigma_v^2 \;\longleftrightarrow\; (h\star h) \sigma_v^2 . \end{eqnarray*}$

In summary, the autocorrelation of filtered white noise $x=h\ast v$ is

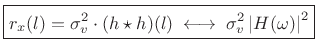$\displaystyle \zbox {r_x(l) = \sigma_v^2\cdot(h\star h)(l) \;\longleftrightarrow\;\sigma_v^2 \left\vert H(\omega)\right\vert^2}$

(7.33)

where $\sigma_v^2$ is the variance of the driving white noise.

In words, the true autocorrelation of filtered white noise equals the autocorrelation of the filter's impulse response times the white-noise variance. (The filter is of course assumed LTI and stable.) In the frequency domain, we have that the true power spectral density of filtered white noise is the squared-magnitude frequency response of the filter scaled by the white-noise variance.

For finite number of observed samples of a filtered white noise process, we may say that the sample autocorrelation of filtered white noise is given by the autocorrelation of the filter's impulse response convolved with the sample autocorrelation of the driving white-noise sequence. For lags much less than the number of observed samples , the driver sample autocorrelation approaches an impulse scaled by the white-noise variance. In the frequency domain, we have that the sample PSD of filtered white noise is the squared-magnitude frequency response of the filter $\vert H(\omega)\vert^2$ scaled by a sample PSD of the driving noise.

We reiterate that every stationary random process may be defined, for our purposes, as filtered white noise.^7.9 As we see from the above, all correlation information is embodied in the filter used.

Example: FIR-Filtered White Noise

Let's estimate the autocorrelation and power spectral density of the ``moving average'' (MA) process

$\displaystyle x(n) = v(n) + v(n-1) + \cdots + v(n-8)$

(7.34)

where is unit-variance white noise.

Since ,

$\displaystyle h\star h = [8,7,6,5,4,3,2,1,0,\ldots]$

(7.35)

for nonnegative lags ( $l\ge0$ ). More completely, we can write

$\displaystyle (h\star h)(l) = \left\{\begin{array}{ll} 8-l, & \vert l\vert<8 \\ [5pt] 0, & \vert l\vert\ge 8. \\ \end{array} \right.$

(7.36)

Thus, the autocorrelation of is a triangular pulse centered on lag 0. The true (unbiased) autocorrelation is given by

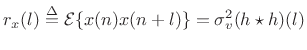$\displaystyle r_x(l) \isdef {\cal E}\{x(n)x(n+l)\} = \sigma_v^2 (h\star h)(l)$

(7.37)

The true power spectral density (PSD) is then

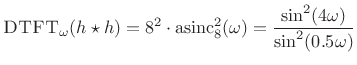$\displaystyle \hbox{\sc DTFT}_\omega(h\star h) = 8^2\cdot\hbox{asinc}^2_{8}(\omega) = \frac{\sin^2(4\omega)}{\sin^2(0.5\omega)}$

(7.38)

Figure 6.3 shows a collection of measured autocorrelations together with their associated smoothed-PSD estimates.

**Figure 6.3:** Averaged sample autocorrelations (biased) and their Fourier transforms (smoothed PSD estimates), for FIR-filtered white noise.
$\includegraphics[width=\twidth]{eps/tcolored}$

Example: Synthesis of 1/F Noise (Pink Noise)

Pink noise ^7.10 or ``1/f noise'' is an interesting case because it occurs often in nature [294],^7.11is often preferred by composers of computer music, and there is no exact (rational, finite-order) filter which can produce it from white noise . This is because the ideal amplitude response of the filter must be proportional to the irrational function $1/\sqrt{f}$ , where denotes frequency in Hz. However, it is easy enough to generate pink noise to any desired degree of approximation, including perceptually exact.

The following Matlab/Octave code generates pretty good pink noise:

Nx = 2^16;  % number of samples to synthesize
B = [0.049922035 -0.095993537 0.050612699 -0.004408786];
A = [1 -2.494956002   2.017265875  -0.522189400];
nT60 = round(log(1000)/(1-max(abs(roots(A))))); % T60 est.
v = randn(1,Nx+nT60); % Gaussian white noise: N(0,1)
x = filter(B,A,v);    % Apply 1/F roll-off to PSD
x = x(nT60+1:end);    % Skip transient response

In the next section, we will analyze the noise produced by the above matlab and verify that its power spectrum rolls off at approximately 3 dB per octave.

Example: Pink Noise Analysis

Let's test the pink noise generation algorithm presented in §6.14.2. We might want to know, for example, does the power spectral density really roll off as ? Obviously such a shape cannot extend all the way to dc, so how far does it go? Does it go far enough to be declared ``perceptually equivalent'' to ideal 1/f noise? Can we get by with fewer bits in the filter coefficients? Questions like these can be answered by estimating the power spectral density of the noise generator output.

Figure 6.4 shows a single periodogram of the generated pink noise, and Figure 6.5 shows an averaged periodogram (Welch's method of smoothed power spectral density estimation). Also shown in each log-log plot is the true 1/f roll-off line. We see that indeed a single periodogram is quite random, although the overall trend is what we expect. The more stable smoothed PSD estimate from Welch's method (averaged periodograms) gives us much more confidence that the noise generator makes high quality 1/f noise.

Note that we do not have to test for stationarity in this example, because we know the signal was generated by LTI filtering of white noise. (We trust the randn function in Matlab and Octave to generate stationary white noise.)