Kaiser Window

Free Books Spectral Audio Signal Processing

Jim Kaiser discovered a simple approximation to the DPSS window based upon Bessel functions [115], generally known as the Kaiser window (or Kaiser-Bessel window).

Definition:

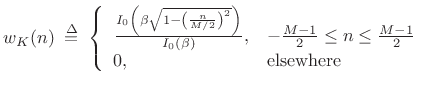$\displaystyle w_K(n) \isdefs \left\{ \begin{array}{ll} \frac{ I_0 \left( \beta \sqrt{ 1 - \left( \frac{n}{M/2}\right)^2} \right)}{ I_0(\beta) }, & -\frac{M-1}{2} \leq n \leq \frac{M-1}{2} \\ 0, & \mbox{elsewhere} \\ \end{array} \right.$

(4.39)

Window transform: The Fourier transform of the Kaiser window

(where

is treated as continuous) is given by^4.11

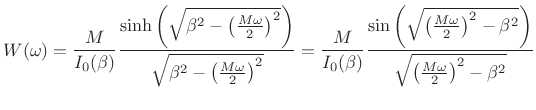$\displaystyle W(\omega) = \frac{M}{I_0(\beta)} \frac{\sinh\left(\sqrt{\beta^2 - \left(\frac{M \omega}{2}\right)^2}\right)} {\sqrt{ \beta^2 - \left(\frac{M\omega}{2}\right)^2}} = \frac{M}{I_0(\beta)} \frac{\sin\left(\sqrt{\left(\frac{M \omega}{2}\right)^2-\beta^2}\right)} {\sqrt{\left(\frac{M\omega}{2}\right)^2 - \beta^2}}$

(4.40)

where

is the zero-order modified Bessel function of the first kind:^4.12

$\displaystyle I_0(x) \isdefs \sum_{k=0}^{\infty} \left[ \frac{\left(\frac{x}{2}\right)^k}{k!} \right]^2$

Notes:

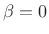
Reduces to rectangular window for $\beta=0$
Asymptotic roll-off is 6 dB/octave
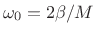
First null in window transform is at $\omega_0=2\beta/M$
Time-bandwidth product 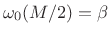$\omega_0 (M/2) = \beta$ radians if bandwidths are measured from 0 to positive band-limit
Full time-bandwidth product 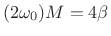$(2\omega_0) M = 4\beta$ radians when frequency bandwidth is defined as main-lobe width out to first null
Sometimes the Kaiser window is parametrized by 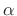$\alpha$ , where

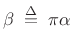
$\displaystyle \beta\isdefs \pi\alpha$ (4.42)

Kaiser Window Beta Parameter

The $\beta$ parameter of the Kaiser window provides a convenient continuous control over the fundamental window trade-off between side-lobe level and main-lobe width. Larger $\beta$ values give lower side-lobe levels, but at the price of a wider main lobe. As discussed in §5.4.1, widening the main lobe reduces frequency resolution when the window is used for spectrum analysis. As explored in Chapter 9, reducing the side lobes reduces ``channel cross talk'' in an FFT-based filter-bank implementation. 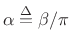The Kaiser beta parameter can be interpreted as 1/4 of the ``time-bandwidth product'' $\Delta t\cdot \Delta \omega$ of the window in radians (seconds times radians-per-second).^4.13 Sometimes the Kaiser window is parametrized by $\alpha\isdef \beta/\pi$ instead of $\beta$ . The $\alpha$ parameter is therefore half the window's time-bandwidth product $\Delta t\cdot \Delta f$ in cycles (seconds times cycles-per-second).

Kaiser Windows and Transforms

Figure 3.24 plots the Kaiser window and its transform for $\alpha = \beta/\pi = 1,2,3$ . Note how increasing $\alpha$ causes the side-lobes to fall away from the main lobe. The curvature at the main lobe peak also decreases somewhat.

**Figure 3.24:** Kaiser window and transform for $\alpha =1,2,3$ .
$\includegraphics[width=\twidth]{eps/kaiser123}$

Figure 3.25 shows a plot of the Kaiser window for various values of $\beta = [0,2,4,6,8,10]$ . Note that for $\beta=0$ , the Kaiser window reduces to the rectangular window.

**Figure 3.25:** The Kaiser window for various values of the time-bandwidth parameter $\beta$ .
$\includegraphics[width=\twidth]{eps/KaiserTBetas}$

Figure 3.26 shows a plot of the Kaiser window transforms for $\beta = [0,2,4,6]$ . For $\beta=0$ (top plot), we see the dB magnitude of the aliased sinc function. As $\beta$ increases the main-lobe widens and the side lobes go lower, reaching almost 50 dB down for $\beta=6$ .

**Figure 3.26:** Kaiser window transform magnitude for various $\beta$ .
$\includegraphics[width=\twidth]{eps/KaiserFBetas}$

Figure 3.27 shows the effect of increasing window length for the Kaiser window. The window lengths are

from the top to the bottom plot. As with all windows, increasing the length decreases the main-lobe width, while the side-lobe level remains essentially unchanged.

**Figure 3.27:** Kaiser window transform magnitudes for various window lengths.
$\includegraphics[width=\twidth]{eps/KaiserFLengths}$

Figure 3.28 shows a plot of the Kaiser window side-lobe level for various values of $\alpha = [0,0.5,1,1.5,\ldots,4]$ . For $\beta=0$ , the Kaiser window reduces to the rectangular window, and we expect the side-lobe level to be about 13 dB below the main lobe (upper-lefthand corner of Fig.3.28). As $\alpha =\beta /\pi$ increases, the dB side-lobe level reduces approximately linearly with main-lobe width increase (approximately a 25 dB drop in side-lobe level for each main-lobe width increase by one sinc-main-lobe).

**Figure 3.28:** Kaiser window side-lobe level for various values of $\alpha =\beta /\pi$ .
$\includegraphics[width=\twidth]{eps/kaiserBeta}$

Minimum Frequency Separation vs. Window Length

The requirements on window length for resolving closely tuned sinusoids was discussed in §5.5.2. This section considers this issue for the Kaiser window. Table 3.1 lists the $\alpha$ parameter required for a Kaiser window to resolve equal-amplitude sinusoids with a frequency spacing of $\Delta\omega$ rad/sample [1, Table 8-9]. Recall from §3.9 that $\alpha$ can be interpreted as half of the time-bandwidth of the window (in cycles).

Table: Kaiser $\alpha$ parameter for various frequency resolutions, assuming an FFT zero-padding factor of at least 3.5.

$\alpha$	$\Delta\omega$
1.5
2.0
2.5
3.0

Kaiser and DPSS Windows Compared

Figure 3.29 shows an overlay of DPSS and Kaiser windows for some different $\alpha$ values. In all cases, the window length was . Note how the two windows become more similar as $\alpha$ increases. The Matlab for computing the windows is as follows:

  w1 = dpss(M,alpha,1);    % discrete prolate spheroidal seq.
  w2 = kaiser(M,alpha*pi); % corresponding kaiser window

**Figure:** Comparison of length 51 DPSS and Kaiser windows for **$\alpha =1,3,5$** .
$\includegraphics[width=\twidth]{eps/dpsstest}$

The following Matlab comparison of the DPSS and Kaiser windows illustrates the interpretation of $\alpha$ as the bin number of the edge of the critically sampled window main lobe, i.e., when the DFT length equals the window length:

format long;
M=17;
alpha=5;
abs(fft([ dpss(M,alpha,1), kaiser(M,pi*alpha)/2]))
ans =
   2.82707022360190   2.50908747431366
   2.00652719015325   1.92930705688346
   0.68469697658600   0.85272343521683
   0.09415916813555   0.19546670371747
   0.00311639169878   0.01773139505899
   0.00000050775691   0.00022611995322
   0.00000003737279   0.00000123787805
   0.00000000262633   0.00000066206722
   0.00000007448708   0.00000034793207
   0.00000007448708   0.00000034793207
   0.00000000262633   0.00000066206722
   0.00000003737279   0.00000123787805
   0.00000050775691   0.00022611995322
   0.00311639169878   0.01773139505899
   0.09415916813555   0.19546670371747
   0.68469697658600   0.85272343521683
   2.00652719015325   1.92930705688346

Finally, Fig.3.30 shows a comparison of DPSS and Kaiser window transforms, where the DPSS window was computed using the simple method listed in §F.1.2. We see that the DPSS window has a slightly narrower main lobe and lower overall side-lobe levels, although its side lobes are higher far from the main lobe. Thus, the DPSS window has slightly better overall specifications, while Kaiser-window side lobes have a steeper roll off.