Free Books    Spectral Audio Signal Processing  

Minimum-Phase Filter Design

Above, we used the Hilbert transform to find the imaginary part of an analytic signal from its real part. A closely related application of the Hilbert transform is constructing a minimum phase [263] frequency response from an amplitude response.

Let $ H(e^{j\omega})$ denote a desired complex, minimum-phase frequency response in the digital domain ($ z$ plane):

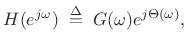$\displaystyle H(e^{j\omega}) \isdefs G(\omega)e^{j\Theta(\omega)},$ (5.23)

and suppose we have only the amplitude response

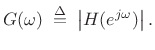$\displaystyle G(\omega) \isdefs \left\vert H(e^{j\omega})\right\vert.$ (5.24)

Then the phase response $ \Theta(\omega)$ can be computed as the Hilbert transform of $ \ln G(\omega)$ . This can be seen by inspecting the log frequency response:

$\displaystyle \ln H(e^{j\omega}) \eqsp \ln G(\omega) + j\Theta(\omega)$ (5.25)

If $ \Theta$ is computed from $ G$ by the Hilbert transform, then $ \ln H(e^{j\omega})$ is an ``analytic signal'' in the frequency domain. Therefore, it has no ``negative times,'' i.e., it is causal. The time domain signal corresponding to a log spectrum is called the cepstrum [263]. It is reviewed in the next section that a frequency response is minimum phase if and only if the corresponding cepstrum is causal [198, Ch. 10], [263, Ch. 11].

Next Section:
Minimum-Phase and Causal Cepstra
Previous Section:
Generalized Window Method