Free Books
   Free Books    Spectral Audio Signal Processing  

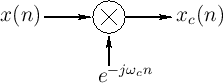
Modulation by a Complex Sinusoid

Figure: System diagram for complex demodulation (frequency-shifting) by $ -\omega _c$ .
\includegraphics{eps/modulation}

Figure 9.12 shows the system diagram for complex demodulation.10.2The input signal $ x(n)$ is multiplied by a complex sinusoid to produce the frequency-shifted result

$\displaystyle x_c(n) = e^{-j\omega_c n} x(n).$ (10.8)

Given a signal expressed as a sum of sinusoids,

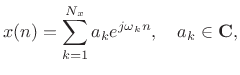$\displaystyle x(n) = \sum_{k=1}^{N_x} a_k e^{j\omega_k n}, \quad a_k\in{\bf C},$ (10.9)

then the demodulation produces

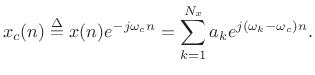$\displaystyle x_c(n) \isdef x(n) e^{-j\omega_c n} = \sum_{k=1}^{N_x} a_k e^{j(\omega_k -\omega_c) n}.$ (10.10)

We see that frequency $ \omega_k$ is down-shifted to $ \omega_k-\omega_c$ . In particular, frequency $ \omega_c$ (the ``center frequency'') is down-shifted to dc.

Next Section:
Making a Bandpass Filter from a Lowpass Filter
Previous Section:
The Running-Sum Lowpass Filter