Sample-Mean Variance

Free Books Spectral Audio Signal Processing

The simplest case to study first is the sample mean:

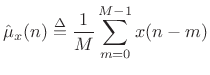$\displaystyle \hat{\mu}_x(n) \isdef \frac{1}{M}\sum_{m=0}^{M-1}x(n-m)$

(C.29)

Here we have defined the sample mean at time as the average of the successive samples up to time --a ``running average''. The true mean is assumed to be the average over any infinite number of samples such as

$\displaystyle \mu_x = \lim_{M\to\infty}\hat{\mu}_x(n)$

(C.30)

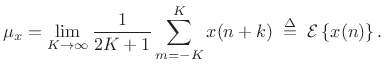$\displaystyle \mu_x = \lim_{K\to\infty}\frac{1}{2K+1}\sum_{m=-K}^{K}x(n+k) \isdefs {\cal E}\left\{x(n)\right\}.$

(C.31)

Now assume $\mu_x=0$ , and let $\sigma_x^2$ denote the variance of the process $x(\cdot)$ , i.e.,

Var $\displaystyle \left\{x(n)\right\} \isdefs {\cal E}\left\{[x(n)-\mu_x]^2\right\} \eqsp {\cal E}\left\{x^2(n)\right\} \eqsp \sigma_x^2$

(C.32)

Then the variance of our sample-mean estimator $\hat{\mu}_x(n)$ can be calculated as follows:

$\begin{eqnarray*} \mbox{Var}\left\{\hat{\mu}_x(n)\right\} &\isdef & {\cal E}\left\{\left[\hat{\mu}_x(n)-\mu_x \right]^2\right\} \eqsp {\cal E}\left\{\hat{\mu}_x^2(n)\right\}\\ &=&{\cal E}\left\{\frac{1}{M}\sum_{m_1=0}^{M-1} x(n-m_1)\, \frac{1}{M}\sum_{m_2=0}^{M-1} x(n-m_2)\right\}\\ &=&\frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_2=0}^{M-1} {\cal E}\left\{x(n-m_1) x(n-m_2)\right\}\\ &=&\frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_2=0}^{M-1} r_x(\vert m_1-m_2\vert) \end{eqnarray*}$

where we used the fact that the time-averaging operator ${\cal E}\left\{\right\}$ is linear, and denotes the unbiased autocorrelation of . If is white noise, then $r_x(\vert m_1-m_2\vert) = \sigma_x^2\delta(m_1-m_2)$ , and we obtain

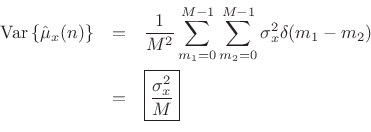
$\begin{eqnarray*}\mbox{Var}\left\{\hat{\mu}_x(n)\right\} &=&\frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_2=0}^{M-1} \sigma_x^2\delta(m_1-m_2)\\ &=&\zbox {\frac{\sigma_x^2}{M}}\\ \end{eqnarray*}$

We have derived that the variance of the -sample running average of a white-noise sequence is given by $\sigma_x^2/M$ , where $\sigma_x^2$ denotes the variance of . We found that the variance is inversely proportional to the number of samples used to form the estimate. This is how averaging reduces variance in general: When averaging independent (or merely uncorrelated) random variables, the variance of the average is proportional to the variance of each individual random variable divided by .