DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Sufficient Condition for Perfect Reconstruction

Above, we found that, for any integer $ 1\leq R\leq N$ which divides $ N$ , a sufficient condition for perfect reconstruction is

$\displaystyle \bold{P}(z)\isdefs \bold{R}(z)\bold{E}(z) \eqsp \bold{I}_N$ (12.59)

and the output signal is then

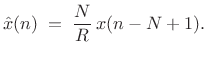$\displaystyle {\hat x}(n) \eqsp \frac{N}{R} \, x(n-N+1).$ (12.60)

More generally, we allow any nonzero scaling and any additional delay:

$\displaystyle \bold{P}(z) \eqsp \bold{R}(z)\bold{E}(z) \eqsp c\, z^{-K}\, \bold{I}_N \protect$ (12.61)

where $ c\neq 0$ is any constant and $ K$ is any nonnegative integer. In this case, the output signal is

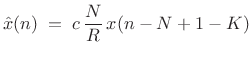$\displaystyle {\hat x}(n) \eqsp c\,\frac{N}{R} \, x(n-N+1-K)$ (12.62)

Thus, given any polyphase matrix $ \bold{E}(z)$ , we can attempt to compute $ \bold{R}(z) = \bold{E}^{-1}(z)$ : If it is stable, we can use it to build a perfect-reconstruction filter bank. However, if $ \bold{E}(z)$ is FIR, $ \bold{R}(z)$ will typically be IIR. In §11.5 below, we will look at paraunitary filter banks, for which $ \bold{R}(z)$ is FIR and paraunitary whenever $ \bold{E}(z)$ is.

Next Section:
Necessary and Sufficient Conditions for Perfect Reconstruction
Previous Section:
Hopping Polyphase Filter Bank