Free Books    Spectral Audio Signal Processing  

Three-Term Blackman-Harris Window

The classic Blackman window of the previous section is a three-term window in the Blackman-Harris family ($ L=2$ ), in which one degree of freedom is used to minimize side-lobe level, and the other is used to maximize roll-off rate. Harris [101, p. 64] defines the three-term Blackman-Harris window as the one which uses both degrees of freedom to minimize side-lobe level. An improved design is given in Nuttall [196, p. 89], and its properties are as follows:

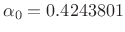
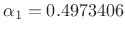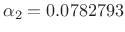  • $ \alpha_0 = 0.4243801$ $ \alpha_1 = 0.4973406$ , and $ \alpha_2 = 0.0782793$ .
  • Side-lobe level 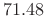$ 71.48$ dB
  • Side lobes roll off 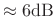$ \approx 6\dB $ per octave in the absence of aliasing (like rectangular and Hamming)
  • All degrees of freedom (scaling aside) are used to minimize side lobes (like Hamming)

Figure 3.14 plots the three-term Blackman-Harris Window and its transform. Figure 3.15 shows the same display for a much longer window of the same type, to illustrate its similarity to the rectangular window (and Hamming window) at high frequencies.

Figure 3.14: Three-term Blackman-Harris window and transform
\includegraphics[width=\twidth]{eps/blackmanHarris3}

Figure 3.15: Longer three-term Blackman-Harris window and transform
\includegraphics[width=\twidth]{eps/blackmanHarris3Long}

Next Section:
Frequency-Domain Implementation of the Blackman-Harris Family
Previous Section:
Matlab for the Classic Blackman Window