Least-squares magic bullets? The Moore-Penrose Pseudoinverse

Posted by Markus Nentwig on Oct 24 2010 under Matlab | Basics | Tips and Tricks   

Hello,

the topic of this brief article is a tool that can be applied to a variety of problems: The Moore-Penrose Pseudoinverse.
While maybe not exactly a magic bullet, it gives us least-squares optimal solutions, and that is under many circumstances the best we can reasonably expect.

I'll demonstrate its use on a short example. More details can be found for example on Wikipedia, or the Matlab documentation for pinv.

The complete Matlab example is here (the link opens a new window).
The purpose of this blog entry is to provide additional information to the example program.

Problem

This picture may look more familar to electronics engineers than we'd like: The blue trace could be a measured signal that has picked up power line hum.

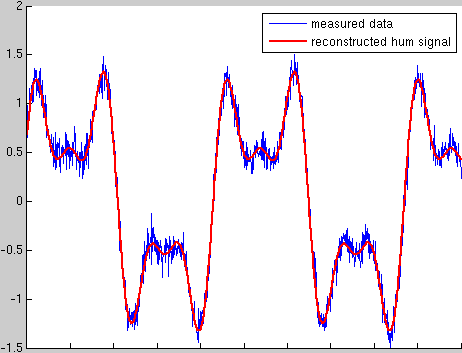
The corresponding variable in the Matlab example is measuredSignal, a column vector with one entry per measured sample.

We'd like to reconstruct the hum signal from the measured signal (red trace), based on the knowledge of possible hum waveforms.

Setting up the equation system

I do know the exact frequency of the power line hum and its harmonics, but I do not know amplitude and phase of each term.
First, I set up a matrix with my "basis" waveforms: index=[1:m]' is a column vector with the sample numbers. The resulting basis matrix has one row per sample, and one column for each of the six candidate waveforms.

Moore-Penrose Pseudoinverse

Next, I calculate the Moore-Penrose Pseudoinverse using pinv(basis), and take a matrix-vector product with the measured signal.
As a result I get a column vector with one coefficient per basis waveform. These coefficients are my least-squares solution, fitting the known waveforms to the original signal:

Next, I reconstruct the hum signal by weighting each basis waveform with its least-squares coefficient and adding the weighted waveforms:

What remains is to subtract the reconstructed hum signal from the measured data.
Voilà, here is the corrected signal:

The picture shows:

• The ideal, undisturbed signal
• The remainder, after subtracting reconstructedHum from measuredSignal
• The difference with regard to the ideal signal (error)

Even though the signal was completely overwhelmed by power line hum in the first picture, we were able to remove the hum almost completely. Not too bad...

For interpretation: The processing has removed as much as possible of the signal energy (sum of squares) by scaling the known waveforms. Or in other words: The remaining signal is the component of the input signal that cannot be "explained" by the basis waveforms.

Of course, if the ideal signal has components that look like power line hum ("can be explained by the basis waveforms"), those will also be removed.

The accuracy increases with the square root of the number of independent samples m. For example, to reduce the error by 3 (10) dB, it takes 4 (100) times more samples. 

On a modern PC, surprisingly large problems can be handled.
A Moore-Penrose Pseudoinverse is a computationally expensive operation. But note that it is applied to the basis waveforms, not the signal. In order to process many signals of the same (or shorter) length, it needs to be computed only once.
Applying it to the measured signal involves only one "dot" (scalar) product between two vectors per coefficient.

Thanks for reading! I hope the example will be useful.

Link

Complete Matlab example, ready to run: here. 

Rate this article:
posted by Markus Nentwig
Markus received his Dipl. Ing. degree in electrical engineering / communications in 1999. Work interests include RF transceiver system design, implementation, modeling and verification. He works as senior architect for Renesas Mobile Europe in Finland.

Previous post by Markus Nentwig: Radio Frequency Distortion Part II: A power spectrum model
Next post by Markus Nentwig: A multiuser waterfilling algorithm
all articles by Markus Nentwig

Would you like to be notified by email when Markus Nentwig publishes a new blog?