Multiplierless Exponential Averaging
This blog discusses an interesting approach to exponential averaging. To begin my story, a traditional exponential averager (also called a "leaky integrator"), shown in Figure 1(a), is commonly used to reduce noise fluctuations that contaminate relatively constant-amplitude signal measurements.
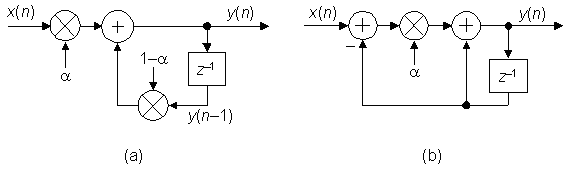
Figure 1 Exponential averaging: (a) standard network; (b) single-multiply network.
That exponential averager's difference equation is
| y(n) = αx(n) + (1 – α)y(n–1) | (1) |
where α is a constant called the averager's weighting factor, in the range 0 < α < 1. The process requires two multiplies per y(n) output sample as shown in Figure 1(a).
As pointed out to me by Vladimir Vassilevsky (http://www.abvolt.com) we can rearrange Eq. (1) to the form
| y(n) = y(n–1) + α[x(n) – y(n–1)] | (2) |
which eliminates one of the averager's multiplies, at the expense of an additional adder, giving us a single-multiply exponential averager shown in Figure 1(b). This neat single-multiply exponential averager maintains the DC (zero Hz) gain of unity exhibited by the traditional two-multiply exponential averager in Figure 1(a).
Contemplating Vassilevsky's single-multiplier exponential averager, I thought about how we could eliminate the multiplier in Figure 1(b) altogether. It is possible to eliminate the multiplier in Figure 1(b) if we place restrictions on the permissible values of α. For example, if α = 0.125 = 1/8, then the output of the multiplier is merely the multiplier's input sample shifted right by three bits.
Thus we can replace the multiplier in Figure 1(b) by a 'binary right shift by L bits' operation as shown in Figure 2(a). In that figure, the 'BRS,L' block means an arithmetic, or hard-wired, Binary Right Shift by L bits. The values for weighting factor α = 1/2L when L is in the range 1 ≤ L ≤ 5 are shown in Figure 2(b). The available exponential averager frequency magnitude responses for those five values for α are shown in Figure 2(c). As it turns out, we can achieve greater flexibility in choosing various values of the averager's weighting factor α. Don't touch that dial!
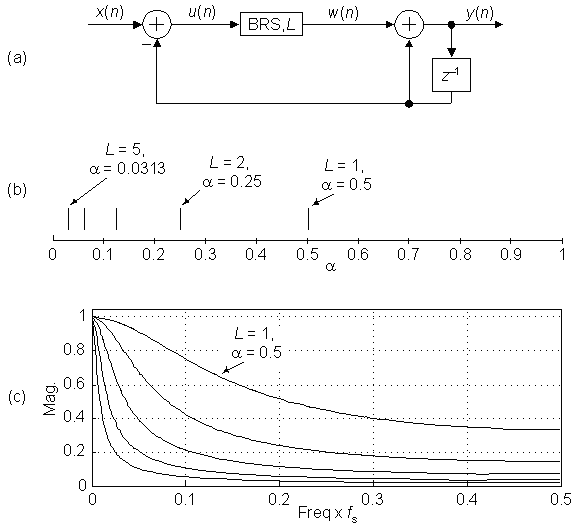
Figure 2 Multiplierless exponential averaging: (a) multiplier-free network; (b) possible values for α when 1≤L≤5; (c) available frequency magnitude responses.
If α takes the form
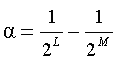 |
(3) |
where L = 0, 1, 2, 3, ..., and M = 1, 2, 3, ..., we can replace the multiplication by α in Figure 1(b) with two binary right shifts and a subtract operation as shown in Figure 3(a).
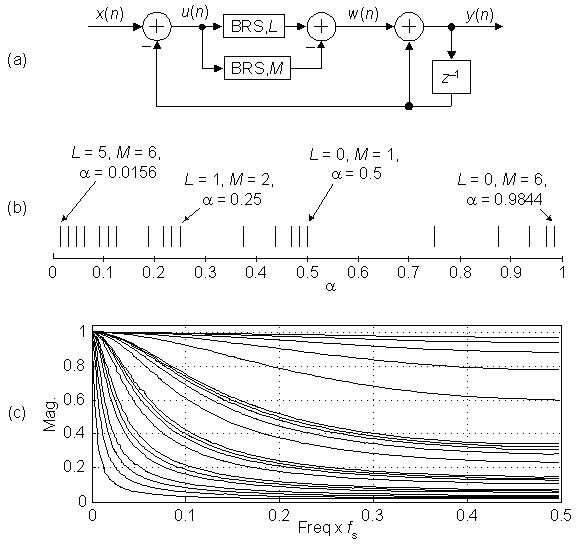
Figure 3 Multiplierless exponential averaging: (a) multiplier-free network; (b) possible values for α when 0≤L≤5 and L+1≤M≤6; (c) available frequency magnitude responses.
For example if L = 2 and M = 5, then from Eq. (3), α = 0.2188. The sequence w(n) = 0.2188u(n) = (1/4 – 1/32)u(n) is computed by subtracting u(n) shifted right by M = 5 bits from u(n) shifted right by L = 2 bits.
The tick marks in Figure 3(b) show the possible values for the weighting factor α over the ranges of 0 ≤ L ≤ 5, where for each L, M is in the range L+1 ≤ M ≤ 6 in Eq. (3). That figure tells us that we have a reasonable selection of α values for our noise-reduction filtering applications. The available exponential averager frequency magnitude responses for those values for α are shown in Figure 3(c), where the top curve corresponds to L = 0 and M = 6 yielding α = 0.9844.
The point of this blog is, for fixed-point implementation of exponential averaging, check to see if your desired α weighting factor can be represented by the difference of various reciprocals of integer powers of two. If so, then binary word shifting enables us to implement a multiplierless exponential averager.
Yes yes, I know—you're wondering, "What about the quantization errors induced by the binary right-shift operations. Well, ...I haven't yet studied that issue.
- Comments
- Write a Comment Select to add a comment
You claim to "eliminate a multiplier" but have not really done so. The shifts and powers of 2 are just a multiply in disguise. Now granted, the "multiplier" you have eliminated might be a dedicated hardware multiplier specifically made for the purpose of multiplying by any number, and that is an advantage when no hardware multiply is available.
This technique can be used to "eliminate a multiplier" in any processing algorithm requiring one.
An additional feature is instead of subtracting, the "M" term from the "L" term, you can add it. This allows additional choices of values for the coefficient without adding terms. For example, if the BRS L term is 1/2, and the BRS M term is 1/8, you can get 5/8 in addition to 3/8 by adding the M term, rather then subtracting it.
Another thing to note when making the change from figure 1(a) to 1(b), single multiply network: the math bit-width increases by 1 bit, including that going into the multiplier. This is important when 8-bit math is being used on 8-bit machine, as it is difficult to get 9 bits without going to 16 bits and "doubling up" in processor instructions not only for the adds, but also for the multiply. Fortunately, there is a neat way around this problem. You split the execution at the front-end adder into 2 branches; one handling the positive result, the other negative. The "ninth bit" is held by the program counter. The last "adder" you either subtract or add the result from the multiply depending upon the sign. This last adder can never overflow, so no 9th bit comes from it. This requires more code, but not more time.

Hi. Is this Brian, my ol' classmate from the University of Akron many decades ago? (Back when the air was clean and sex was dirty.)
Binary right/left shifting does implement a very limited kind of multiplication, but I wouldn't refer to a binary shifting register as a conventional (traditional) "multiplier". That's why I used a rectangular symbol in Figure 2 rather the the conventional circular multiplier symbol in Figure 1. I suppose we could debate this topic.
Your suggestion of adding the "M term to the L term" is a very astute idea for increasing the available choices of alpha in Figure 3. Good job Brian. (Now why didn't I think of that(!)?)
As for the possibility of binary overflow in the Figure 2(a) and Figure 3(a) implementations, I agree with you.
Yes it is! Regarding your 2nd paragraph, what you are implementing is exactly a multiplier with limited "1" terms in the multiplier. You are skipping adds on "some" of the shifts.
There is another problem with this low pass filter circuit when you do it in limited bit-width. The output will never settle to the input no long how long you wait. For example, with 8 bit math and a multiplier coefficient of 1/16th, as soon as the difference between the output and input gets less then 16, approach stops. The filter has a huge hysteresis of +/- 15 (+/- 8 if you round). If you implement the multiplier with a lookup table, the fix is easy. After calculating the table, you modify it by putting 1's in all the zeros of the table except for the case when the input is zero. Now when the difference gets less then 16, the output will step toward the input. I have added a non-linearity, but it is minor as it only acts when the difference is small.
I have used this (along with my code-splitting trick) in my various robots and Halloween animations to smooth motions.

Brian, calm down. No need to get excited here. I can't make sense out of the first paragraph of your above post. My software modeling, using integer data, of my Figure 3(a) filter does not exhibit any anomalies similar to what you describe in your confusing second paragraph.
I won't spend any more time reading your complaints. All I can suggest is: Keep your life simple Brian. If you don't want to use the Figure 3(a) filter, then don't use it.
Please hear me out. This is not intended as a criticism for your filter design; it is a "watch out!" when you are using limited bit-width math. I will give example: let both input and output be settled at 0, and K (multiplier) be 1/16th. Let input go to 25 (00011001b). This is difference into shifter, which shifts right 4 times, giving 00000001b. Output goes to 1. On 9 successive iterations, output goes 2, 3, 4, 5, 6, 7, 8, 9, 10. On next iteration, input to shifter is 25-10 = 15 (00001111b). After 4 right shifts, you get 0. No further adds occur to the output, which remains at 10 for all future iterations.
You can minimize this "deadband" by adding more precision "inside" the filter, both in the shifter and the [Z-1] memory cell. For this case, you would need 4 more bits. The larger the "multiplier" coefficient, the fewer bits you need to add, so it is better to work "closer to the Nyquist limit".

Hi Brian. OK. Yes yes. You are correct. With a pure DC input, like your all 25's input sequence, unlike a floating-point implementation the fixed-point implementation's output will not asymptotically approach the correct all 25's DC input level.
And as often happens with other 8-bit fixed-point IIR filters, unwanted nonlinear behavior can occur when we try to implement a very narrowband filter by placing the filter's pole close to the z-plane's unit circle. And those unpleasant nonlinear effects are particularly bad when the input sequence is low in amplitude.
Thanks to your comments I intend to add a postscript to my blog discussing this nonlinearity topic and possibly suggest that fixed-point exponential averagers not be implemented in less than 16-bit fixed-point filters.

Wow, it is a small world. As it turns out, I also know you Brian, although somewhat indirectly through your brother Jeff. This is all through a common work affiliation, circa 88 to 90, when I was a co-op student. With the clues of bpark + Halloween + Akron + DSP discussions, it essentially eliminated any other possibility. Great to hear from you and hope you are well.

The fixed-point or integer math technique illustrated in Rick's article has a formal name, Canonic Signed Digit. It's always helpful to have a shorthand way to refer to something. Great article as always Rick, explained ever so clearly.
https://www.allaboutcircuits.com/technical-article...

Hi kschutz.
Thanks for the useful web links!
To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:

























