Sign in

username:

password:



Not a member?

Search Online Books



Search tips

Free Online Books



Chapters

See Also

Embedded SystemsFPGAElectronics

Physical Audio Signal Processing
    Digital Waveguide Theory
       The Digital Waveguide Oscillator
          Eigenstructure
             Damping and Tuning Parameters

Chapter Contents:

Search Physical Audio Signal Processing

  

Book Index | Global Index

Would you like to be notified by email when Julius Orion Smith III publishes a new entry into his blog?

  

Damping and Tuning Parameters

The tuning and damping of the resonator impulse response are governed by the relation

$\displaystyle {\lambda_i}= e^{\frac{T}{\tau}} e^{\pm j\omega T} $

where $ T$ denotes the sampling interval, $ \tau $ is the time constant of decay, and $ \omega $ is the frequency of oscillation in radians per second. The eigenvalues are presumed to be complex, which requires, from Eq.$ \,$(C.144),

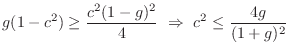
$\displaystyle g(1-c^2) \geq\frac{c^2(1-g)^2}{4} \,\,\Rightarrow\,\,c^2 \leq \frac{4g}{(1+g)^2} $

To obtain a specific decay time-constant $ \tau $, we must have

\begin{eqnarray*} e^{-2T/\tau} &=& \left\vert{\lambda_i}\right\vert^2 = c^2\left... ...left[g(1-c^2) - c^2\left(\frac{1-g}{2}\right)^2\right]\\ &=& g \end{eqnarray*}

Therefore, given a desired decay time-constant $ \tau $ (and the sampling interval $ T$), we may compute the damping parameter $ g$ for the digital waveguide resonator as

$\displaystyle \zbox {g = e^{-2T/\tau}.} $

Note that this conclusion follows directly from the determinant analysis of Eq.$ \,$(C.140), provided it is known that the poles form a complex-conjugate pair.

To obtain a desired frequency of oscillation, we must solve

\begin{eqnarray*} \theta = \omega T &=& \tan^{-1}\left[\frac{\sqrt{g(1-c^2) - [... ...,\tan^2{\theta} &=& \frac{g(1-c^2) - [c(1-g)/2]^2}{[c(1+g)/2]^2} \end{eqnarray*}

for $ c$, which yields

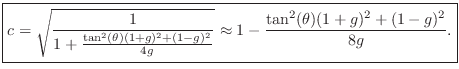
$\displaystyle \zbox { c= \sqrt{\frac{1}{1 + \frac{\tan^2(\theta)(1+g)^2+(1-g)^2}{4g}}} \approx 1 - \frac{\tan^2(\theta)(1+g)^2 + (1-g)^2}{8g}. } $

Note that this reduces to $ c=\cos(\theta)$ when $ g=1$ (undamped case).

Previous: Eigenstructure
Next: Eigenvalues in the Undamped Case

Order a Hardcopy of Physical Audio Signal Processing

About the Author: Julius Orion Smith III
Julius Smith's background is in electrical engineering (BS Rice 1975, PhD Stanford 1983). He is presently Professor of Music and Associate Professor (by courtesy) of Electrical Engineering at Stanford's Center for Computer Research in Music and Acoustics (CCRMA), teaching courses and pursuing research related to signal processing applied to music and audio systems. See http://ccrma.stanford.edu/~jos/ for details.


Comments

No comments yet for this page


Add a Comment
You need to login before you can post a comment (best way to prevent spam). ( Not a member? )