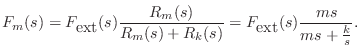Mechanical Impedance Analysis

Impedance analysis is commonly used to analyze electrical circuits [110]. By means of equivalent circuits, we can use the same analysis methods for mechanical systems.

For example, referring to Fig.7.9, the Laplace transform of the force on the spring is given by the so-called voltage divider relation:^8.2

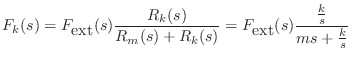
$\displaystyle F_k(s) = F_{\mbox{ext}}(s) \frac{R_k(s)}{R_m(s)+R_k(s)} = F_{\mbox{ext}}(s) \frac{\frac{k}{s}}{ms+\frac{k}{s}}$

Similarly, the Laplace transform of the force on the mass

is given by

$\displaystyle F_m(s) = F_{\mbox{ext}}(s) \frac{R_m(s)}{R_m(s)+R_k(s)} = F_{\mbox{ext}}(s) \frac{ms}{ms+\frac{k}{s}}. \protect$

(8.1)

As a simple application, let's find the motion of the mass , after time zero, given that the input force is an impulse at time 0:

$\displaystyle f_{\mbox{ext}}(t)=\delta(t) \;\leftrightarrow\; F_{\mbox{ext}}(s)=1$

Then, by the ``voltage divider'' relation Eq. $\,$ (7.1), the Laplace transform of the mass force

after time 0 is given by

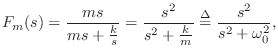
$\displaystyle F_m(s) = \frac{ms}{ms+\frac{k}{s}} = \frac{s^2}{s^2+\frac{k}{m}} \isdef \frac{s^2}{s^2+\omega_0^2},$

where we have defined $\omega_0^2\isdef k/m$ . The mass velocity Laplace transform is then

$\begin{eqnarray*} V_m(s) &=& \frac{F_m(s)}{ms} \;=\; \frac{1}{m} \cdot \frac{s}{... ...}\right]\\ [5pt] &\leftrightarrow& \frac{1}{m} \cos(\omega_0 t). \end{eqnarray*}$

Thus, the impulse response of the mass oscillates sinusoidally with radian frequency $\omega_0=\sqrt{k/m}$ , and amplitude . The velocity starts out maximum at time , which makes physical sense. Also, the momentum transferred to the mass at time 0 is $m\,v(0+) = 1$ ; this is also expected physically because the time-integral of the applied force is 1 (the area under any impulse $\delta(t)$ is 1).

Previous: Spring-Mass System
Next: General One-Ports

Order a Hardcopy of Physical Audio Signal Processing

About the Author: Julius Orion Smith III
Julius Smith's background is in electrical engineering (BS Rice 1975, PhD Stanford 1983). He is presently Professor of Music and Associate Professor (by courtesy) of Electrical Engineering at Stanford's Center for Computer Research in Music and Acoustics (CCRMA), teaching courses and pursuing research related to signal processing applied to music and audio systems. See http://ccrma.stanford.edu/~jos/ for details.

Sign in

Search Online Books

Free Online Books

Sponsor

Chapters

See Also

Physical Audio Signal Processing
    Lumped Models
       One-Port Network Theory
          Mechanical Impedance Analysis