Critically Sampled Perfect Reconstruction Filter Banks
A Perfect Reconstruction (PR) filter bank is any filter bank
whose reconstruction is the original signal, possibly delayed, and
possibly scaled by a constant [287]. In this context,
critical sampling (also called ``maximal downsampling'') means
that the downsampling factor is the same as the number of filter
channels. For the STFT, this implies ![]() (with
(with ![]() allowed for
Portnoff windows).
allowed for
Portnoff windows).
As derived in Chapter 8, the Short-Time Fourier
Transform (STFT) is a PR filter bank whenever the Constant-OverLap-Add
(COLA) condition is met by the analysis window ![]() and the hop size
and the hop size
![]() . However, only the rectangular window case with no
zero-padding is critically sampled (OLA hop size = FBS downsampling
factor =
. However, only the rectangular window case with no
zero-padding is critically sampled (OLA hop size = FBS downsampling
factor = ![]() ). Perceptual audio compression algorithms such as MPEG
audio coding are based on critically sampled filter banks, for obvious
reasons. It is important to remember that we normally do not require
critical sampling for audio analysis, digital audio effects, and music
applications; instead, we normally need critical sampling only when
compression is a requirement. Thus, when compression is not a
requirement, we are normally interested in oversampled filter
banks. The polyphase representation is useful in that case as
well. In particular, we will obtain some excellent insights into the
aliasing cancellation that goes on in such downsampled filter
banks (including STFTs with hop sizes
). Perceptual audio compression algorithms such as MPEG
audio coding are based on critically sampled filter banks, for obvious
reasons. It is important to remember that we normally do not require
critical sampling for audio analysis, digital audio effects, and music
applications; instead, we normally need critical sampling only when
compression is a requirement. Thus, when compression is not a
requirement, we are normally interested in oversampled filter
banks. The polyphase representation is useful in that case as
well. In particular, we will obtain some excellent insights into the
aliasing cancellation that goes on in such downsampled filter
banks (including STFTs with hop sizes ![]() ), as the next section
makes clear.
), as the next section
makes clear.
Two-Channel Critically Sampled Filter Banks
Figure 11.15 shows a simple two-channel band-splitting filter bank,
followed by the corresponding synthesis filter bank which
reconstructs the original signal (we hope) from the two channels. The
analysis filter ![]() is a half-band lowpass filter, and
is a half-band lowpass filter, and ![]() is a complementary half-band highpass filter. The synthesis filters
is a complementary half-band highpass filter. The synthesis filters
![]() and
and ![]() are to be derived. Intuitively, we expect
are to be derived. Intuitively, we expect
![]() to be a lowpass that rejects the upper half-band due to the
upsampler by 2, and
to be a lowpass that rejects the upper half-band due to the
upsampler by 2, and ![]() should do the same but then also
reposition its output band as the upper half-band, which can be
accomplished by selecting the upper of the two spectral images in the
upsampler output.
should do the same but then also
reposition its output band as the upper half-band, which can be
accomplished by selecting the upper of the two spectral images in the
upsampler output.
The outputs of the two analysis filters in Fig.11.15 are
| (12.16) |
Using the results of §11.1, the signals become, after downsampling,
![$\displaystyle V_k(z) \eqsp \frac{1}{2}\left[X_k(z^{1/2}) + X_k(-z^{1/2})\right], \; k=0,1.$](http://www.dsprelated.com/josimages_new/sasp2/img1988.png) |
(12.17) |
After upsampling, the signals become
![$\displaystyle \frac{1}{2}[X_k(z) + X_k(-z)]$](http://www.dsprelated.com/josimages_new/sasp2/img1990.png) |
|||
![$\displaystyle \frac{1}{2}[H_k(z)X(z) + H_k(-z)X(-z)],\; k=0,1.$](http://www.dsprelated.com/josimages_new/sasp2/img1991.png) |
After substitutions and rearranging, we find that the output
For perfect reconstruction, we require the aliasing term to be zero. For ideal half-band filters cutting off at
In this case, synthesis filter
Referring again to (11.18), we see that we also need the
non-aliased term to be of the form
where
| (12.21) |
That is, for perfect reconstruction, we need, in addition to aliasing cancellation, that the non-aliasing term reduce to a constant gain
Let
![]() denote
denote ![]() . Then both constraints can be expressed in
matrix form as follows:
. Then both constraints can be expressed in
matrix form as follows:
![$\displaystyle \left[\begin{array}{cc} H_0 & H_1 \\ [2pt] {\tilde H}_0 & {\tilde H}_1 \end{array}\right]\left[\begin{array}{c} F_0 \\ [2pt] F_1 \end{array}\right]\eqsp \left[\begin{array}{c} c \\ [2pt] 0 \end{array}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img2013.png) |
(12.22) |
Substituting the aliasing-canceling choices for ![]() and
and ![]() from
(11.19) into the filtering-cancellation constraint (11.20), we
obtain
from
(11.19) into the filtering-cancellation constraint (11.20), we
obtain
The filtering-cancellation constraint is almost satisfied by ideal zero-phase half-band filters cutting off at
Amplitude-Complementary 2-Channel Filter Bank
A natural choice of analysis filters for our two-channel critically sampled filter bank is an amplitude-complementary lowpass/highpass pair, i.e.,
| (12.24) |
where we impose the unity dc gain constraint
Substituting the COLA constraint into the filtering and aliasing cancellation constraint (11.23) gives
![\begin{eqnarray*}
g\,z^{-d} &=& H_0(z)\left[1-H_0(-z)\right] - \left[1-H_0(z)\right]H_0(-z) \\ [5pt]
&=& H_0(z) - H_0(-z)\\ [5pt]
\;\longleftrightarrow\;\quad a(n) &=& h_0(n) - (-1)^n h_0(n) \\ [5pt]
&=& \left\{\begin{array}{ll}
0, & \hbox{$n$\ even} \\ [5pt]
2h_0(n), & \hbox{$n$\ odd} \\
\end{array} \right.
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2021.png)
Thus, we find that even-indexed terms of the impulse response are
unconstrained, since they subtract out in the constraint, while,
for perfect reconstruction, exactly one odd-indexed term
must be nonzero in the lowpass impulse response ![]() . The
simplest choice is
. The
simplest choice is
![]() .
.
Thus, we have derived that the lowpass-filter impulse-response for channel 0 can be anything of the form
or
| (12.26) |
etc. The corresponding highpass-filter impulse response is then
| (12.27) |
The first example (11.25) above goes with the highpass filter
| (12.28) |
and similarly for the other example.
The above class of amplitude-complementary filters can be characterized in general as follows:
![\begin{eqnarray*}
H_0(z) &=& E_0(z^2) + h_0(o) z^{-o}, \quad E_0(1)+h_0(o)\eqsp 1, \, \hbox{$o$\ odd}\\ [5pt]
H_1(z) &=& 1-H_0(z) \eqsp 1 - E_0(z^2) - h_0(o) z^{-o}
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2028.png)
In summary, we see that an amplitude-complementary
lowpass/highpass analysis filter pair yields perfect reconstruction
(aliasing and filtering cancellation) when there is exactly one
odd-indexed term in the impulse response of ![]() .
.
Unfortunately, the channel filters are so constrained in form that it
is impossible to make a high quality lowpass/highpass pair. This
happens because ![]() repeats twice around the unit circle. Since
we assume real coefficients, the frequency response,
repeats twice around the unit circle. Since
we assume real coefficients, the frequency response,
![]() is magnitude-symmetric about
is magnitude-symmetric about
![]() as
well as
as
well as ![]() . This is not good since we only have one degree of
freedom,
. This is not good since we only have one degree of
freedom,
![]() , with which we can break the
, with which we can break the ![]() symmetry
to reduce the high-frequency gain and/or boost the low-frequency gain.
This class of filters cannot be expected to give high quality lowpass
or highpass behavior.
symmetry
to reduce the high-frequency gain and/or boost the low-frequency gain.
This class of filters cannot be expected to give high quality lowpass
or highpass behavior.
To achieve higher quality lowpass and highpass channel filters, we will need to relax the amplitude-complementary constraint (and/or filtering cancellation and/or aliasing cancellation) and find another approach.
Haar Example
Before we leave the case of amplitude-complementary, two-channel,
critically sampled, perfect reconstruction filter banks, let's see
what happens when ![]() is the simplest possible lowpass filter
having unity dc gain, i.e.,
is the simplest possible lowpass filter
having unity dc gain, i.e.,
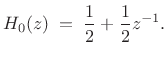 |
(12.29) |
This case is obtained above by setting
| (12.30) |
Choosing
![\begin{eqnarray*}
H_0(z) &=& \frac{1}{2} + \frac{1}{2}z^{-1} \eqsp E_0(z^2)+z^{-1}E_1(z^2)\\ [5pt]
H_1(z) &=& 1-H_0(z) \eqsp \frac{1}{2} - \frac{1}{2}z^{-1} \eqsp E_0(z^2)-z^{-1}E_1(z^2)\\ [5pt]
F_0(z) &=& \;\;\, H_1(-z) \eqsp \frac{1}{2} + \frac{1}{2}z^{-1} \eqsp \;\;\,H_0(z)\\ [5pt]
F_1(z) &=& -H_0(-z) \eqsp -\frac{1}{2} + \frac{1}{2}z^{-1} \eqsp -H_1(z).
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2038.png)
Thus, both the analysis and reconstruction filter banks are scalings
of the familiar Haar filters (``sum and difference'' filters
![]() ). The frequency responses are
). The frequency responses are
![\begin{eqnarray*}
H_0(e^{j\omega}) &=&\;\;\,F_0(e^{j\omega}) \eqsp \frac{1}{2} + \frac{1}{2}e^{-j\omega}\eqsp e^{-j\frac{\omega}{2}} \cos\left(\frac{\omega}{2}\right)\\ [5pt]
H_1(e^{j\omega}) &=& -F_0(e^{j\omega}) \eqsp \frac{1}{2} - \frac{1}{2}e^{-j\omega}\eqsp j e^{-j\frac{\omega}{2}} \sin\left(\frac{\omega}{2}\right)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2040.png)
which are plotted in Fig.11.16.
Polyphase Decomposition of Haar Example
Let's look at the polyphase representation for this example. Starting
with the filter bank and its reconstruction (see Fig.11.17), the
polyphase decomposition of ![]() is
is
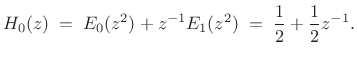 |
(12.31) |
Thus,
| (12.32) |
We may derive polyphase synthesis filters as follows:
![\begin{eqnarray*}
\hat{X}(z) &=& \left[F_0(z)H_0(z) + F_1(z)H_1(z)\right] X(z)\\
&=& \left[\left(\frac{1}{2} + \frac{1}{2}z^{-1}\right)H_0(z) + \left(-\frac{1}{2}+\frac{1}{2}z^{-1}\right)H_1(z)\right]X(z)\\
&=& \frac{1}{2}\left\{\left[H_0(z)-H_1(z)\right] + z^{-1}\left[H_0(z) + H_1(z)\right]\right\}X(z)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2046.png)
The polyphase representation of the filter bank and its reconstruction can now be drawn as in Fig.11.18. Notice that the reconstruction filter bank is formally the transpose of the analysis filter bank [263]. A filter bank that is inverted by its own transpose is said to be an orthogonal filter bank, a subject to which we will return §11.3.8.
![\includegraphics[width=\twidth]{eps/poly2chan}](http://www.dsprelated.com/josimages_new/sasp2/img2047.png) |
Commuting the downsamplers (using the noble identities from
§11.2.5), we obtain Figure 11.19. Since
![]() , this is simply the OLA form of an
STFT filter bank for
, this is simply the OLA form of an
STFT filter bank for ![]() , with
, with ![]() , and rectangular
window
, and rectangular
window
![]() . That is, the DFT size, window length, and hop
size are all 2, and both the DFT and its inverse are simply
sum-and-difference operations.
. That is, the DFT size, window length, and hop
size are all 2, and both the DFT and its inverse are simply
sum-and-difference operations.
Quadrature Mirror Filters (QMF)
The well studied subject of Quadrature Mirror Filters (QMF) is entered by imposing the following symmetry constraint on the analysis filters:
That is, the filter for channel 1 is constrained to be a
In the time domain, the QMF constraint (11.33) becomes
![]() , i.e., all odd-index coefficients are negated. If
, i.e., all odd-index coefficients are negated. If ![]() is a lowpass filter cutting off near
is a lowpass filter cutting off near
![]() (as is typical),
then
(as is typical),
then ![]() is a complementary highpass filter. The exact cut-off
frequency can be adjusted along with the roll-off rate to provide a
maximally constant frequency-response sum.
is a complementary highpass filter. The exact cut-off
frequency can be adjusted along with the roll-off rate to provide a
maximally constant frequency-response sum.
Two-channel QMFs have been around since at least 1976 [51], and appear to be the first critically sampled perfect reconstruction filter banks. Moreover, the Princen-Bradley filter bank, the initial foundation of MPEG audio as we now know it, was conceived as the Fourier dual of QMFs [214]. Historically, the term QMF applied only to two-channel filter banks having the QMF symmetry constraint (11.33). Today, the term ``QMF filter bank'' may refer to more general PR filter banks with any number of channels and not obeying (11.33) [287].
Combining the QMF symmetry constraint with the aliasing-cancellation constraints, given by
![\begin{eqnarray*}
F_0(z) &=& \quad\! H_1(-z) \eqsp \quad\! H_0(z)\\ [5pt]
F_1(z) &=& -H_0(-z) \eqsp -H_1(z),
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2055.png)
the perfect reconstruction requirement reduces to
Now, all four filters are determined by
It is easy to show using the polyphase representation of ![]() (see
[287]) that the only causal FIR QMF analysis filters yielding
exact perfect reconstruction are two-tap FIR filters of the
form
(see
[287]) that the only causal FIR QMF analysis filters yielding
exact perfect reconstruction are two-tap FIR filters of the
form

where ![]() and
and ![]() are constants, and
are constants, and ![]() and
and ![]() are integers.
Therefore, only weak channel filters are available in the QMF case
[
are integers.
Therefore, only weak channel filters are available in the QMF case
[
![]() ], as we saw in the amplitude-complementary case
above. On the other hand, very high quality IIR solutions are
possible. See [287, pp. 201-204] for details. In
practice, approximate ``pseudo QMF'' filters are more practical, which
only give approximate perfect reconstruction. We'll return to this
topic in §11.7.1.
], as we saw in the amplitude-complementary case
above. On the other hand, very high quality IIR solutions are
possible. See [287, pp. 201-204] for details. In
practice, approximate ``pseudo QMF'' filters are more practical, which
only give approximate perfect reconstruction. We'll return to this
topic in §11.7.1.
The scaled Haar filters, which we saw gave perfect reconstruction in the amplitude-complementary case, are also examples of a QMF filter bank:
![\begin{eqnarray*}
H_0(z) &=& 1 + z^{-1}\\ [5pt]
H_1(z) &=& 1 - z^{-1}
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2063.png)
In this example, ![]() , and
, and ![]() .
.
Linear Phase Quadrature Mirror Filter Banks
Linear phase filters delay all frequencies by equal amounts, and this
is often a desirable property in audio and other applications. A
filter phase response is linear in ![]() whenever its impulse
response
whenever its impulse
response ![]() is symmetric, i.e.,
is symmetric, i.e.,
| (12.35) |
in which case the frequency response can be expressed as
| (12.36) |
Substituting this into the QMF perfect reconstruction constraint (11.34) gives
![$\displaystyle g\,e^{-j\omega d} \eqsp e^{-j\omega N}\left[ \left\vert H_0(e^{j\omega})\right\vert^2 - (-1)^N\left\vert H_0(e^{j(\pi-\omega)})\right\vert^2\right].$](http://www.dsprelated.com/josimages_new/sasp2/img2068.png) |
(12.37) |
When
![$\displaystyle g\,z^{-j\omega d} \eqsp e^{-j\omega N}\left[ \left\vert H_0(e^{j\omega})\right\vert^2 + \left\vert H_0(e^{j(\pi-\omega)}\right\vert^2\right].$](http://www.dsprelated.com/josimages_new/sasp2/img2069.png) |
(12.38) |
We see that perfect reconstruction is obtained in the linear-phase case whenever the analysis filters are power complementary. See [287] for further details.
Conjugate Quadrature Filters (CQF)
A class of causal, FIR, two-channel, critically sampled, exact perfect-reconstruction filter-banks is the set of so-called Conjugate Quadrature Filters (CQF). In the z-domain, the CQF relationships are
| (12.39) |
In the time domain, the analysis and synthesis filters are given by
![\begin{eqnarray*}
h_1(n) &=& -(-1)^n h_0(L-1-n) \\ [5pt]
f_0(n) &=& h_0(L-1-n) \\ [5pt]
f_1(n) &=& -(-1)^n h_0(n) \eqsp - h_1(L-1-n).
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2071.png)
That is,
![]() for the lowpass channel, and each highpass
channel filter is a modulation of its lowpass counterpart by
for the lowpass channel, and each highpass
channel filter is a modulation of its lowpass counterpart by ![]() .
Again, all four analysis and synthesis filters are determined by the
lowpass analysis filter
.
Again, all four analysis and synthesis filters are determined by the
lowpass analysis filter ![]() . It can be shown that this is an
orthogonal filter bank. The analysis filters
. It can be shown that this is an
orthogonal filter bank. The analysis filters ![]() and
and
![]() are power complementary, i.e.,
are power complementary, i.e.,
| (12.40) |
or
| (12.41) |
where
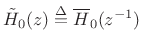 denotes the
paraconjugate of
denotes the
paraconjugate of | (12.42) |
The power symmetric case was introduced by Smith and Barnwell in 1984 [272]. With the CQF constraints, (11.18) reduces to
Let
![]() , such that
, such that ![]() is a spectral factor of
the half-band filter
is a spectral factor of
the half-band filter ![]() (i.e.,
(i.e.,
![]() is a nonnegative power
response which is lowpass, cutting off near
is a nonnegative power
response which is lowpass, cutting off near
![]() ). Then,
(11.43) reduces to
). Then,
(11.43) reduces to
The problem of PR filter design has thus been reduced to designing one half-band filter
A simple design of an FIR half-band filter would be to window a sinc function:
![$\displaystyle p(n) \eqsp \frac{\hbox{sin}[\pi n/2]}{\pi n/2}w(n)$](http://www.dsprelated.com/josimages_new/sasp2/img2087.png) |
(12.45) |
where
Note that as a result of (11.43), the CQF filters are power complementary. That is, they satisfy
| (12.46) |
Also note that the filters
- FIR
- orthogonal
- linear phase
By relaxing ``orthogonality'' to ``biorthogonality'', it becomes possible to obtain FIR linear phase filters in a critically sampled, perfect reconstruction filter bank. (See §11.9.)
Orthogonal Two-Channel Filter Banks
Recall the reconstruction equation for the two-channel, critically sampled, perfect-reconstruction filter-bank:
![\begin{eqnarray*}
\hat{X}(z) &=& \frac{1}{2}[H_0(z)F_0(z) + H_1(z)F_1(z)]X(z)
\nonumber\\ [5pt]
&+& \frac{1}{2}[H_0(-z)F_0(z) + H_1(-z)F_1(z)]X(-z)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2089.png)
This can be written in matrix form as
![$\displaystyle \hat{X}(z) \eqsp \frac{1}{2} \left[\begin{array}{c} F_0(z) \\ [2pt] F_1(z) \end{array}\right]^{T} \left[\begin{array}{cc} H_0(z) & H_0(-z) \\ [2pt] H_1(z) & H_1(-z) \end{array}\right] \left[\begin{array}{c} X(z) \\ [2pt] X(-z) \end{array}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img2090.png) |
(12.47) |
where the above
| (12.48) |
where
 denotes the
paraconjugate of
denotes the
paraconjugate of
It turns out orthogonal filter banks give perfect reconstruction filter banks for any number of channels. Orthogonal filter banks are also called paraunitary filter banks, which we'll study in polyphase form in §11.5 below. The AC matrix is paraunitary if and only if the polyphase matrix (defined in the next section) is paraunitary [287].
Next Section:
Perfect Reconstruction Filter Banks
Previous Section:
Polyphase Decomposition








![\begin{psfrags}
% latex2html id marker 29839\psfrag{x(n)}{\normalsize $x(n)$}\psfrag{x}{\normalsize $x$}\psfrag{(n)}{\normalsize $(n)$}\psfrag{y}{\normalsize $y$}\psfrag{v}{\normalsize $v$}\psfrag{H}{\normalsize $H$}\psfrag{F}{\normalsize $F$}\psfrag{z}{\normalsize $z$}\begin{figure}[htbp]
\includegraphics[width=\twidth]{eps/cqf}
\caption{Two-channel critically sampled filter bank.}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img1986.png)
![$\displaystyle \frac{1}{2}\left[H_0(z)F_0(z) + H_1(z)F_1(z)\right]X(z)$](http://www.dsprelated.com/josimages_new/sasp2/img1994.png)
![$\displaystyle \frac{1}{2}\left[H_0(-z)F_0(z) + H_1(-z)F_1(z)\right]X(-z)
\protect$](http://www.dsprelated.com/josimages_new/sasp2/img1996.png)
![\includegraphics[width=\twidth]{eps/haar}](http://www.dsprelated.com/josimages_new/sasp2/img2041.png)
![\begin{psfrags}
% latex2html id marker 29979\psfrag{x(n)}{\normalsize $x(n)$}\psfrag{x}{\normalsize $x$}\psfrag{(n)}{\normalsize $(n)$}\psfrag{y}{\normalsize $y$}\psfrag{v}{\normalsize $v$}\psfrag{H}{\normalsize $H$}\psfrag{F}{\normalsize $F$}\psfrag{z}{\normalsize $z$}\begin{figure}[htbp]
\includegraphics[width=\twidth]{eps/cqfcopy}
\caption{Two-channel polyphase filter bank and inverse.}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img2042.png)
![\includegraphics[width=\twidth]{eps/poly2chanfast}](http://www.dsprelated.com/josimages_new/sasp2/img2048.png)
![$\displaystyle \hat{X}(z) \eqsp \frac{1}{2}\left[H_0(z)H_0(z^{-1}) + H_0(-z)H_0(-z^{-1})\right]X(z) \protect$](http://www.dsprelated.com/josimages_new/sasp2/img2079.png)
![$\displaystyle \hat{X}(z) \eqsp \frac{1}{2}\left[P(z) + P(-z)\right]X(z) \eqsp -z^{-(L-1)}X(z)$](http://www.dsprelated.com/josimages_new/sasp2/img2084.png)












