Allpass Examples
- The simplest allpass filter is a unit-modulus gain
where
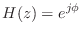
 can be any phase value. In the real case
can be any phase value. In the real case  can only be 0 or
can only be 0 or  , in which case
, in which case
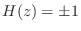 .
.
- A lossless FIR filter can consist only of a single nonzero tap:
for some fixed integer
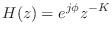
 , where
, where  is again some constant phase,
constrained to be 0 or
is again some constant phase,
constrained to be 0 or  in the real-filter case. Since we are
considering only causal filters here,
in the real-filter case. Since we are
considering only causal filters here, 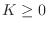 . As a special case of
this example, a unit delay
. As a special case of
this example, a unit delay
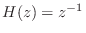 is a simple FIR allpass filter.
is a simple FIR allpass filter.
- The transfer function of every finite-order, causal,
lossless IIR digital filter (recursive allpass filter) can be written
as
where
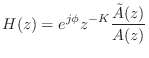
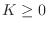 ,
and
,
and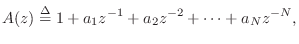
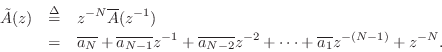
We may think of
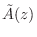 as the flip of
as the flip of  . For example,
if
. For example,
if
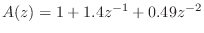 , we have
, we have
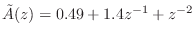 . Thus,
. Thus,
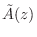 is obtained from
is obtained from  by simply reversing the order of the
coefficients and conjugating them when they are complex.
by simply reversing the order of the
coefficients and conjugating them when they are complex.
- For analog filters, the general finite-order allpass
transfer function is
where
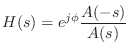
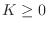 ,
,
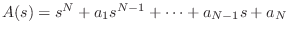 .
The polynomial
.
The polynomial  can be obtained by negating every other
coefficient in
can be obtained by negating every other
coefficient in  , and multiplying by
, and multiplying by 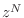 . In analog, a pure
delay of
. In analog, a pure
delay of 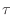 seconds corresponds to the transfer function
which is infinite order. Given a pole
seconds corresponds to the transfer function
which is infinite order. Given a pole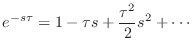
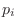 (root of
(root of 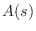 at
at 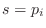 ),
the polynomial
),
the polynomial  has a root at
has a root at 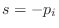 . Thus, the poles and
zeros can be paired off as a cascade of terms such as
The frequency response of such a term is
. Thus, the poles and
zeros can be paired off as a cascade of terms such as
The frequency response of such a term is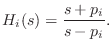 which is obviously unit magnitude.
which is obviously unit magnitude.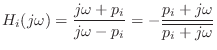
Next Section:
Paraunitary FiltersC.4
Previous Section:
Elementary Filter Problems




















