Analysis of Nonlinear Filters

Free Books Introduction to Digital Filters

There is no general theory of nonlinear systems. A nonlinear system with memory can be quite surprising. In particular, it can emit any output signal in response to any input signal. For example, it could replace all music by Beethoven with something by Mozart, etc. That said, many subclasses of nonlinear filters can be successfully analyzed:

A nonlinear, memoryless, time-invariant ``black box'' can be ``mapped out'' by measuring its response to a scaled impulse 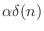$\alpha\delta(n)$ at each amplitude 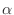$\alpha$ , where 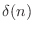$\delta (n)$ denotes the impulse signal ( $[1,0,0,\ldots]$ ).
A memoryless nonlinearity followed by an LTI filter can similarly be characterized by a stack of impulse-responses indexed by amplitude (look up dynamic convolution on the Web).

One often-used tool for nonlinear systems analysis is Volterra series [4]. A Volterra series expansion represents a nonlinear system as a sum of iterated convolutions:

$\displaystyle y = h_0 + h_1 \ast x + ((h_{2,n} \ast x)_n \ast x) + \cdots$

Here

is the input signal,

is the output signal, and the impulse-response replacements

are called Volterra kernels. The special notation $((h_{2,n} \ast x)_n \ast x)$ indicates that the second-order kernel

is fundamentally two-dimensional, meaning that the third term above (the first nonlinear term) is written out explicitly as

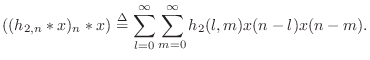
$\displaystyle ((h_{2,n} \ast x)_n \ast x) \isdef \sum_{l=0}^\infty\sum_{m=0}^\infty h_2(l,m) x(n-l)x(n-m).$

Similarly, the third-order kernel

is three-dimensional, in general. In principle, every nonlinear system can be represented by its (typically infinite) Volterra series expansion. The method is most successful when the kernels rapidly approach zero as order increases.

In the special case for which the Volterra expansion reduces to

$\displaystyle y = h_0 + h_1 \ast x + h_2 \ast x \ast x + \cdots\,,$