Complex and Trigonometric Identities

Free Books Introduction to Digital Filters

This section gives a summary of some of the more useful mathematical identities for complex numbers and trigonometry in the context of digital filter analysis. For many more, see handbooks of mathematical functions such as Abramowitz and Stegun [2].

The symbol $\isdef$ means ``is defined as''; stands for a complex number; and , $\theta$ , , and stand for real numbers. The quantity is used below to denote $\tan(\theta/2)$ .

Complex Numbers

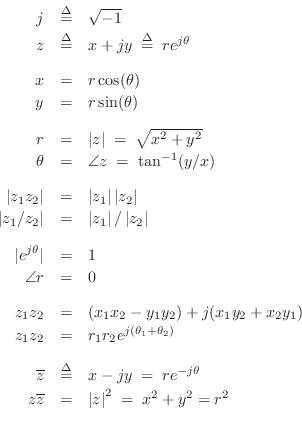
$\begin{displaymath} \begin{array}{rclrcl} \mrr {j}{\isdef }{\sqrt{-1}}{z}{\isdef... ...z}}{=}{\left\vert z\right\vert^2 \;=\; x^2+y^2=r^2} \end{array}\end{displaymath}$

The Exponential Function

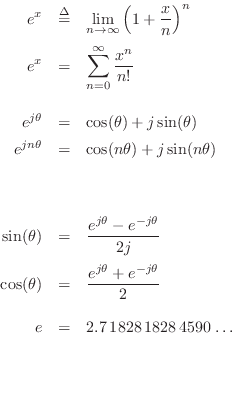
$\begin{eqnarray*} \mrr {e^x}{\isdef }{\displaystyle\lim_{n\to\infty}\left(1+\fra... ...{-j\theta}}{2}} \mrr {e}{=}{2.7\,1828\,1828\,4590\,\ldots}{}{}{} \end{eqnarray*}$

Trigonometric Identities

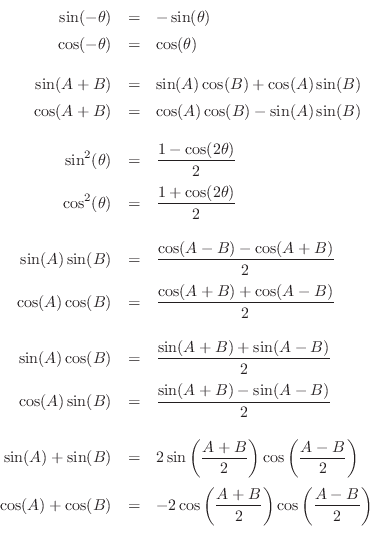
$\begin{eqnarray*} \mr {\sin(-\theta)}{-\sin(\theta)}% {\cos(-\theta)}{\cos(\thet... ...{-2\cos\left(\frac{A+B}{2}\right)\cos\left(\frac{A-B}{2}\right)} \end{eqnarray*}$

Trigonometric Identities, Continued

$\begin{eqnarray*} \mr {\sin(A)-\sin(B)}{2\cos\left(\frac{A+B}{2}\right)\sin\left... ...cos(A)\cos(B)}}% {\tan(A+B)}{\frac{\tan(A+B)}{1-\tan(A)\tan(B)}} \end{eqnarray*}$

Half-Angle Tangent Identities

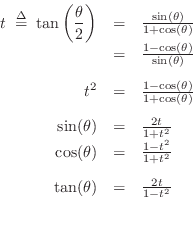
$\begin{displaymath} \begin{array}{rclrcl} \mr {t\;\isdef \;\tan\left(\frac{\thet... ...1+t^2}}% \mrone {\tan(\theta)}{=}{\frac{2t}{1-t^2}} \end{array}\end{displaymath}$

Next Section:
A Sum of Sinusoids at the Same Frequency is Another Sinusoid at that Frequency
Previous Section:
Signal Representation and Notation