DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Convolution Theorem

The convolution theorem for z transforms states that for any (real or) complex causal signals $ x$ and $ y$, convolution in the time domain is multiplication in the $ z$ domain, i.e.,

$\displaystyle \zbox {x\ast y \;\leftrightarrow\; X\cdot Y} $

or, using operator notation,

$\displaystyle {\cal Z}_z\{x \ast y\} \;=\; X(z)Y(z), $

where $ X(z)\isdef {\cal Z}_z(x)$, and $ Y(z)\isdef {\cal Z}_z(y)$. (See [84] for a development of the convolution theorem for discrete Fourier transforms.)


Proof:

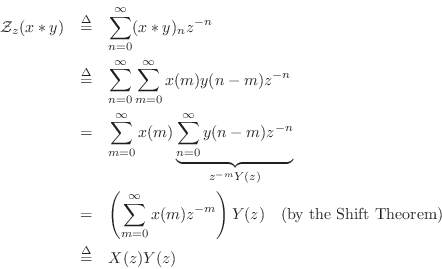
\begin{eqnarray*} {\cal Z}_z(x\ast y) &\isdef & \sum_{n=0}^{\infty}(x\ast y)_n z... ...(by the Shift Theorem)}\\ &\isdef & X(z)Y(z) % \quad\pfendmath \end{eqnarray*}

The convolution theorem provides a major cornerstone of linear systems theory. It implies, for example, that any stable causal LTI filter (recursive or nonrecursive) can be implemented by convolving the input signal with the impulse response of the filter, as shown in the next section.

Next Section:
Series Case
Previous Section:
Shift Theorem