DSPRelated.com
Free Books
The 2025 DSP Online Conference
   Free Books    Introduction to Digital Filters  

Example: The General Biquad PFE

The general second-order case with $ M=N=2$ (the so-called biquad section) can be written when $ b_0\ne 0$ as

$\displaystyle H(z) \eqsp g\frac{1 + b_1 z^{-1}+ b_2 z^{-2}}{1 + a_1 z^{-1}+ a_2 z^{-2}}. $

To perform a partial fraction expansion, we need to extract an order 0 (length 1) FIR part via long division. Let $ d=z^{-1}$ and rewrite $ H(z)$ as a ratio of polynomials in $ d$:

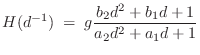
$\displaystyle H(d^{-1}) \eqsp g\frac{b_2 d^2 + b_1 d + 1 }{a_2 d^2 + a_1 d + 1} $

Then long division gives % For typesetting long division --- NEEDED WITHIN THE MAKEIMAGE ENV? % (raw TeX,... ...} & & b_1-\frac{b_2}{a_2}a_1 & 1-\frac{b_2}{a_2} & \end{array}\end{displaymath}
yielding

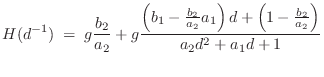
$\displaystyle H(d^{-1}) \eqsp g\frac{b_2}{a_2} + g\frac{\left(b_1-\frac{b_2}{a_2}a_1\right)d+ \left(1-\frac{b_2}{a_2}\right)}{a_2d^2 + a_1d + 1} $

or

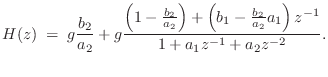
$\displaystyle H(z) \eqsp g\frac{b_2}{a_2} + g\frac{\left(1-\frac{b_2}{a_2}\right) +\left(b_1-\frac{b_2}{a_2}a_1\right)z^{-1}}{1 + a_1z^{-1}+ a_2z^{-2}}. $

The delayed form of the partial fraction expansion is obtained by leaving the coefficients in their original order. This corresponds to writing $ H(z)$ as a ratio of polynomials in $ z$:

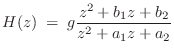
$\displaystyle H(z) \eqsp g\frac{z^2 + b_1 z + b_2 }{z^2 + a_1 z + a_2} $

Long division now looks like % For typesetting long division --- NEEDED WITHIN THE MAKEIMAGE ENV?\begin{dis... ...rule width 22\digitwidth}} & & b_1-a_1 & b_2-a_2 & \end{array}\end{displaymath}
giving

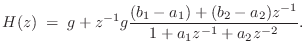
$\displaystyle H(z) \eqsp g + z^{-1}g\frac{(b_1-a_1) + (b_2-a_2)z^{-1}}{1 + a_1 z^{-1}+ a_2 z^{-2}}. $

Numerical examples of partial fraction expansions are given in §6.8.8 below. Another worked example, in which the filter $ y(n) = x(n) + 0.5^3 x(n-3) - 0.9^5 y(n-5)$ is converted to a set of parallel, second-order sections is given in §3.12. See also §9.2 regarding conversion to second-order sections in general, and §G.9.1 (especially Eq.$ \,$(G.22)) regarding a state-space approach to partial fraction expansion.

Next Section:
Dealing with Repeated Poles Analytically
Previous Section:
Series Combination is Commutative
The 2025 DSP Online Conference