DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Example

It is easy to classify completely all first-order FIR filters:

$\displaystyle H(z) = 1 + h_1 z^{-1} $

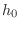
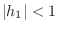
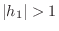
where we have normalized $ h_0$ to 1 for simplicity. We have a single zero at $ z=-h_1$. If $ \left\vert h_1\right\vert< 1$, the filter is minimum phase. If $ \left\vert h_1\right\vert>1$, it is maximum phase. Note that the minimum-phase case is the one in which the impulse response $ [1,h_1,0,\ldots]$ decays instead of grows. It can be shown that this is a general property of minimum-phase sequences, as elaborated in the next section.

Next Section:
Units
Previous Section:
Software for Linear-Phase Filter Design