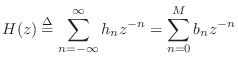DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

FIR Transfer Function

The transfer function of an FIR filter is given by the z transform of its impulse response. This is true for any LTI filter, as discussed in Chapter 6. For FIR filters in particular, we have, from Eq.$ \,$(5.6),

$\displaystyle H(z) \isdef \sum_{n=-\infty}^{\infty} h_n z^{-n} = \sum_{n=0}^M b_n z^{-n} \protect$ (6.8)

Thus, the transfer function of every length $ N=M+1$ FIR filter is an $ M$th-order polynomial in $ z^{-1}$.

Next Section:
FIR Order
Previous Section:
Causal FIR Filters