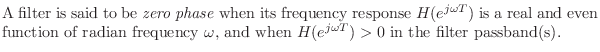Free Books Introduction to Digital Filters

Filters Preserving Phase

In this chapter, linear phase and zero phase filters are defined and discussed.

Linear-Phase Filters
(Symmetric Impulse Responses)

A linear-phase filter is typically used when a causal filter is needed to modify a signal's magnitude-spectrum while preserving the signal's time-domain waveform as much as possible. Linear-phase filters have a symmetric impulse response, e.g.,

$\displaystyle h(n) = h(N-1-n), \quad n=0,1,2,\ldots,N-1.$

The symmetric-impulse-response constraint means that linear-phase filters must be FIR filters, because a causal recursive filter cannot have a symmetric impulse response.

We will show that every real symmetric impulse response corresponds to a real frequency response times a linear phase term $e^{-j\alpha\omega T}$ , where $\alpha = (N-1)/2$ is the slope of the linear phase. Linear phase is often ideal because a filter phase of the form $\Theta(\omega) = - \alpha \omega T$ corresponds to phase delay

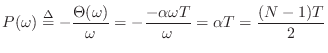
$\displaystyle P(\omega) \isdef - \frac{\Theta(\omega)}{\omega} = - \frac{-\alpha\omega T}{\omega} = \alpha T = \frac{(N-1)T}{2}$

and group delay

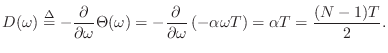
$\displaystyle D(\omega) \isdef - \frac{\partial}{\partial \omega}\Theta(\omega... ...l}{\partial \omega}\left(-\alpha\omega T\right) = \alpha T = \frac{(N-1)T}{2}.$

That is, both the phase and group delay of a linear-phase filter are equal to

samples of plain delay at every frequency. Since a length

FIR filter implements

samples of delay, the value

is exactly half the total filter delay. Delaying all frequency components by the same amount preserves the waveshape as much as possible for a given amplitude response.

Zero-Phase Filters
(Even Impulse Responses)

A zero-phase filter is a special case of a linear-phase filter in which the phase slope is $\alpha=0$ . The real impulse response of a zero-phase filter is even.^11.1 That is, it satisfies

$\displaystyle h(n) = h(-n), \quad n\in{\bf Z}$

Note that every even signal is symmetric, but not every symmetric signal is even. To be even, it must be symmetric about time 0.

A zero-phase filter cannot be causal (except in the trivial case when the filter is a constant scale factor $h(n)=g\delta(n)$ ). However, in many ``off-line'' applications, such as when filtering a sound file on a computer disk, causality is not a requirement, and zero-phase filters are often preferred.

It is a well known Fourier symmetry that real, even signals have real, even Fourier transforms [84]. Therefore,

$\textstyle \parbox{0.8\textwidth}{\emph{a real, even impulse response corresponds to a real, \\ even frequency response.}}$

This follows immediately from writing the DTFT of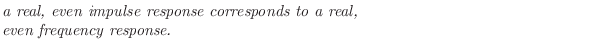

in terms of a cosine and sine transform:

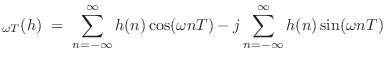
$\displaystyle H(e^{j\omega T}) \eqsp$ DTFT $\displaystyle _{\omega T}(h) \eqsp \sum_{n=-\infty}^\infty h(n) \cos(\omega nT) - j \sum_{n=-\infty}^\infty h(n) \sin(\omega nT)$

Since

is even, cosine is even, and sine is odd; and since even times even is even, and even times odd is odd; and since the sum over an odd function is zero, we have that

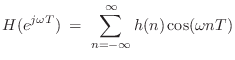
$\displaystyle H(e^{j\omega T}) \eqsp \sum_{n=-\infty}^\infty h(n) \cos(\omega nT)$

for any real, even impulse-response

. Thus, the frequency response $H(e^{j\omega T})$ is a real, even function of $\omega$ .

A real frequency response has phase zero when it is positive, and phase $\pi$ when it is negative. Therefore, we define a zero-phase filter as follows:

$\textstyle \parbox{0.8\textwidth}{A filter is said to be \emph{zero phase} when... ... frequency $\omega$, and when $H(e^{j\omega T})>0$\ in the filter passband(s).}$

Recall from §7.5.2 that a passband is defined as a frequency band that is ``passed'' by the filter, i.e., the filter is not designed to minimize signal amplitude in the band. For example, in a lowpass filter with cut-off frequency $\omega_c$ rad/s, the passband is $\omega\in[-\omega_c,\omega_c]$ .

$\pi$ -Phase Filters

Under our definition, a zero-phase filter always has a real, even impulse response [ ], but not every real, even, impulse response is a zero-phase filter. For example, if is zero phase, then is not; however, we could call a `` $\pi$ -phase filter'' if we like (a zero-phase filter in series with a sign inversion).

Phase $\pi$ in the Stopband

Practical zero-phase filters are zero-phase in their passbands, but may switch between 0 and $\pi$ in their stopbands (as illustrated in the upcoming example of Fig.10.2). Thus, typical zero-phase filters are more precisely described as piecewise constant-phase filters, where the constant phase is 0 in all passbands, and $\pi$ over various intervals within stopbands. Similarly, practical ``linear phase'' filters are typically truly linear phase across their passbands, but typically exhibit discontinuities by $\pi$ radians in their stopband(s). As long as the stopbands are negligible, which is the goal by definition, the $\pi$ -phase regions can be neglected completely.

Example Zero-Phase Filter Design

Figure 10.1 shows the impulse response and frequency response of a length 11 zero-phase FIR lowpass filter designed using the Remez exchange algorithm.^11.2 The matlab code for designing this filter is as follows:

N = 11;                % filter length - must be odd
b = [0 0.1 0.2 0.5]*2; % band edges
M = [1  1   0   0 ];   % desired band values
h = remez(N-1,b,M);    % Remez multiple exchange design

The impulse response h is returned in linear-phase form, so it must be left-shifted

samples to make it zero phase.

**Figure 10.1:** Impulse response and frequency response of a length 11 zero-phase FIR lowpass filter. Note that the frequency response is real because the filter is zero phase. Also plotted (in dashed lines) are the desired passband and stopband gains.
$\includegraphics[width=\twidth ]{eps/remezexa}$

Figure 10.2 shows the amplitude and phase responses of the FIR filter designed by remez. The phase response is zero throughout the passband and transition band. However, each zero-crossing in the stopband results in a phase jump of $\pi$ radians, so that the phase alternates between zero and $\pi$ in the stopband. This is typical of practical zero-phase filters.

**Figure:** Amplitude response and phase response of the length 11 zero-phase FIR lowpass filter in Fig.10.1.
$\includegraphics[width=\twidth ]{eps/remezexb}$

Elementary Zero-Phase Filter Examples

A practical zero-phase filter was illustrated in Figures 10.1 and 10.2. Some simple general cases are as follows:

The trivial (non-)filter 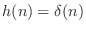$h(n)=\delta(n)$ has frequency response 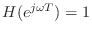$H(e^{j\omega T})=1$ , which is zero phase for all $\omega$ .
Every second-order zero-phase FIR filter has an impulse response of the form

$\displaystyle h(n) \eqsp b_{1}\delta(n+1) + b_0\delta(n) + b_1 \delta(n-1),$
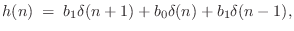
where the coefficients 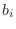are assumed real. The transfer function of the general, second-order, real, zero-phase filter is

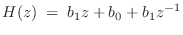$\displaystyle H(z) \eqsp b_{1}z + b_0 + b_1 z^{-1}$
and the frequency response is

$\displaystyle H(e^{j\omega T}) \eqsp b_{1}e^{j\omega T}+ b_0 + b_1 e^{-j\omega T}\eqsp b_0 + 2 b_1 \cos(\omega T)$
which is real for all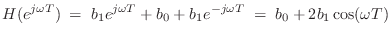 $\omega$ .
Extending the previous example, every order 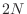zero-phase real FIR filter has an impulse response of the form

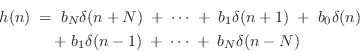
$\begin{eqnarray*} \lefteqn{ h(n) \eqsp b_{N}\delta(n+N) \;+\; \cdots \;+\; b_{... ...ots & & \;+\; b_1 \delta(n-1) \;+\; \cdots \;+\; b_N\delta(n-N) \end{eqnarray*}$

and frequency response

$\displaystyle H(e^{j\omega T}) \eqsp b_0 \;+\; 2 \sum_{k=1}^N b_k \cos(k\omega T)$
which is clearly real whenever the coefficients 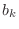are real.
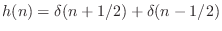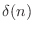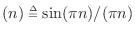There is no first-order (length 2) zero-phase filter, because, to be even, its impulse response would have to be proportional to $h(n)=\delta(n+1/2) + \delta(n-1/2)$ . Since the bandlimited digital impulse signal $\delta (n)$ is ideally interpolated using bandlimited interpolation [91,84], giving samples of sinc $(n)\isdeftext \sin(\pi n)/(\pi n)$ --the unit-amplitude sinc function having zero-crossings on the integers, we see that sampling on the integers yields an IIR filter:

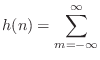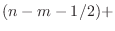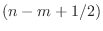
$\displaystyle h(n) = \sum_{m=-\infty}^{\infty}$ sinc $\displaystyle (n-m-1/2) +$ sinc $\displaystyle (n-m+1/2)$
Similarly, there are no odd-order (even-length) zero-phase filters.

Odd Impulse Reponses

Note that odd impulse responses of the form are closely related to zero-phase filters (even impulse responses). This is because another Fourier symmetry relation is that the DTFT of an odd sequence is purely imaginary [84]. In practice, Hilbert transform filters and differentiators are often implemented as odd FIR filters [68]. A purely imaginary frequency response can be divided by to give a real frequency response. As a result, filter-design software for one case is easily adapted to the other [68].

Equivalently, an odd impulse response can be multiplied by in the time domain to yield a purely imaginary impulse response that is Hermitian. Hermitian signals have real Fourier transforms [84]. Therefore, a Hermitian impulse response gives a filter having a phase response that is either zero or $\pi$ at each frequency.

Symmetric Linear-Phase Filters

As stated at the beginning of this chapter, the impulse response of every causal, linear-phase, FIR filter is symmetric:

$\displaystyle h(n) = h(N-1-n), \quad n=0,1,2,\ldots,N-1.$

Assume that

is odd. Then the filter

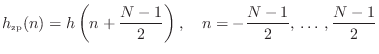
$\displaystyle h_{\hbox{\tiny zp}}(n) = h\left(n+\frac{N-1}{2}\right), \quad n=-\frac{N-1}{2},\,\ldots\,,\frac{N-1}{2}$

is a zero-phase filter. Thus, every odd-length linear-phase filter can be expressed as a delay of some zero-phase filter,

$\displaystyle h(n) = h_{\hbox{\tiny zp}}\left(n-\frac{N-1}{2}\right), \quad n=0,1,2,\ldots, N-1.$

By the shift theorem for z transforms (§6.3), the transfer function of a linear-phase filter is

$\displaystyle H(z) = z^{-\frac{N-1}{2}}H_{\hbox{zp}}(z)$

and the frequency response is

$\displaystyle H(e^{j\omega T}) = e^{-j\omega \frac{N-1}{2}T}H_{\hbox{zp}}(e^{j\omega T})$

which is a linear phase term times $H_{\hbox{zp}}(e^{j\omega T})$ which is real. Since $H_{\hbox{zp}}(e^{j\omega T})$ can go negative, the phase response is

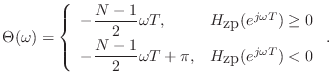
$\displaystyle \Theta(\omega) = \left\{\begin{array}{ll} \displaystyle-\frac{N-... ...-1}{2}\omega T + \pi, & H_{\hbox{zp}}(e^{j\omega T})<0 \\ \end{array}\right..$

For frequencies $\omega$ at which $H_{\hbox{zp}}(e^{j\omega T})$ is nonnegative, the phase delay and group delay of a linear-phase filter are simply half its length:

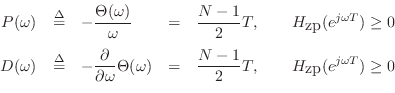
$\begin{displaymath} \begin{array}{rclrcl} P(\omega) &\isdef & -\displaystyle\fra... ...2} T, \qquad H_{\hbox{zp}}(e^{j\omega T})\geq0\\ \end{array}\end{displaymath}$

Simple Linear-Phase Filter Examples

The example of §10.2.1 was in fact a linear-phase FIR filter design example. The resulting causal finite impulse response was left-shifted (``advanced'' in time) to make it zero phase.
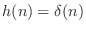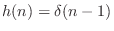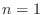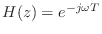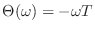While the trivial ``bypass filter'' $h(n)=\delta(n)$ is zero-phase (§10.2.2), the ``bypass filter with a unit delay,'' $h(n) = \delta(n-1)$ is linear phase. It is (trivially) symmetric about time , and the frequency response is $H(z) = e^{-j\omega T}$ , which is a pure linear phase term $\Theta(\omega)=-\omega T$ having a slope of 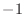samples (radians per radians-per-sample), or 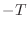seconds (radians per radians-per-second). The phase- and group-delays are each 1 sample at every frequency.
The impulse response of the simplest lowpass filter studied in Chapter 1 was 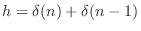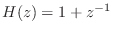$h = \delta(n) + \delta(n-1)$ [ $H(z)=1+z^{-1}$ ]. Since this impulse response is symmetric about time 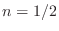samples, it is linear phase, and $\Theta(\omega) = -\omega T/2$ , as derived in Chapter 1. The phase delay and group delay are both 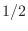sample at each frequency. Note that even-length linear-phase filters cannot be time-shifted (without interpolation) to create a corresponding zero-phase filter. However, they can be shifted to make a near-zero-phase filter that has a phase delay and group delay equal to half a sample at all passband frequencies.

Software for Linear-Phase Filter Design

The Matlab Signal Processing Toolbox covers many applications with the following functions:

$\displaystyle \begin{tabular}{rl} \texttt{remez()} & (optimal Chebyshev linear-... ...or general FIR (or IIR)\\ & filter design \cite[page 50]{JOST}). \end{tabular}$

All of these functions except firls are implemented in the free, open-source, Octave Forge collection as well.

Methods for FIR filter design are discussed in the fourth book of the music signal processing series [87], and classic references include [64,68]. There is also quite a large research literature on this subject.

Antisymmetric Linear-Phase Filters

In the same way that odd impulse responses are related to even impulse responses, linear-phase filters are closely related to antisymmetric impulse responses of the form , . An antisymmetric impulse response is simply a delayed odd impulse response (usually delayed enough to make it causal). The corresponding frequency response is not strictly linear phase, but the phase is instead linear with a constant offset (by $\pm\pi/2$ ). Since an affine function is any function of the form $f(\omega)=\alpha \omega + \beta$ , where $\alpha$ and $\beta$ are constants, an antisymmetric impulse response can be called an affine-phase filter. These same remarks apply to any linear-phase filter that can be expressed as a time-shift of a $\pi$ -phase filter (i.e., it is inverting in some passband). However, in practice, all such filters may be loosely called ``linear-phase'' filters, because they are designed and implemented in essentially the same way [68].

Note that truly linear-phase filters have both a constant phase delay and a constant group delay. Affine-phase filters, on the other hand, have a constant group delay, but not a constant phase delay.

Forward-Backward Filtering

There are no linear-phase recursive filters because a recursive filter cannot generate a symmetric impulse response. However, it is possible to implement a zero-phase filter offline using a recursive filter twice. That is, if the entire input signal $x(\cdot)$ is stored in a computer memory or hard disk, for example, then we can apply a recursive filter both forward and backward in time. Doing this squares the amplitude response of the filter and zeros the phase response.

To show this analytically, let denote the output of the first filtering operation (which we'll take to be ``forward'' in time in the normal way), and let be the impulse response of the recursive filter. Then we have

$\displaystyle v(n) = (h\ast x)(n),$

where

is the input signal at sample

. For the second pass, we ``flip''

to obtain

and apply the filter again:

$\displaystyle w(n) = (h\ast$ FLIP $\displaystyle (v))(n)$

The final output is then this result flipped:

$\displaystyle y =$ FLIP $\displaystyle (w) =$ FLIP $\displaystyle (h\ast$ FLIP $\displaystyle (v)) =$ FLIP $\displaystyle (h)\ast v,$

where the last simplification tells us that flipping the input and output signals is equivalent to flipping the impulse response instead. Putting all these operations together, we have

$\displaystyle y(n) =$ FLIP $\displaystyle _n(h\ast$ FLIP $\displaystyle (h\ast x)) = ($ FLIP $\displaystyle (h)\ast (h\ast x))(n).$

By the flip theorem for z transforms, we have that the z transform of FLIP

is $X(z^{-1})$ :

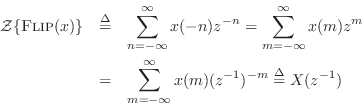
$\begin{eqnarray*} {\cal Z}\{\mbox{{\sc Flip}}(x)\} &\isdef & \sum_{n=-\infty}^\i... ... &=& \sum_{m=-\infty}^\infty x(m) (z^{-1})^{-m} \isdef X(z^{-1}) \end{eqnarray*}$

Using this result and applying the convolution theorem (§6.3) twice gives the z transform

$\displaystyle Y(z) = H(z^{-1})[H(z)X(z)].$

On the unit circle, this reduces to, for real filters

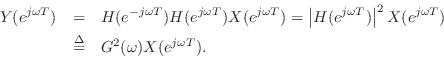
$\begin{eqnarray*} Y(e^{j\omega T}) &=& H(e^{-j\omega T})H(e^{j\omega T})X(e^{j\o... ...rt^2 X(e^{j\omega T})\\ &\isdef & G^2(\omega) X(e^{j\omega T}). \end{eqnarray*}$

If the filter were complex, then we would need to conjugate its coefficients when running it backwards.

In summary, we have thus shown that forward-backward filtering squares the amplitude response and zeros the phase response. Note also that the phase response is truly zero, never alternating between zero and $\pi$ . No matter what nonlinear phase response $\Theta(\omega)$ a filter may have, this phase is completely canceled out by forward and backward filtering. The amplitude response, on the other hand, is squared. For simple bandpass filters (including lowpass, highpass, etc.), for which the desired gain is 1 in the passband and 0 in the stopband, squaring the amplitude response usually improves the response, because the ``stopband ripple'' (deviation from 0) is squared, thereby doubling the stopband attenuation in dB. On the other hand, passband ripple (deviation from 1) is only doubled by the squaring (because $(1+\epsilon)^2 = 1+2\epsilon + \epsilon^2\approx 1+2\epsilon$ ).

A Matlab example of forward-backward filtering is presented in §11.6 (in Fig.11.1).

Phase Distortion at Passband Edges

For many applications (such as lowpass, bandpass, or highpass filtering), the most phase dispersion occurs at the extreme edge of the passband (i.e., in the vicinity of cut-off frequencies). This phenomenon was clearly visible in the example of Fig.7.6.4. Only filters without feedback can have exactly linear phase (unless forward-backward filtering is feasible), and such filters generally need many more multiplies for a given specification on the amplitude response $G(\omega)$ [68]. One should keep in mind that phase dispersion near a cut-off frequency (or any steep transition in the amplitude response) usually appears as ringing near that frequency in the time domain. (This can be heard in the upcoming matlab example of §11.6, Fig.11.1.)

For musical purposes, $G(\omega)$ , or the effect that a filter has on the magnitude spectrum of the input signal, is usually of primary interest. This is true for all ``instantaneous'' filtering operations such as tone controls, graphical equalizers, parametric equalizers, formant filter banks, shelving filters, and the like. (Elementary examples in this category are discussed in Appendix B.) Notable exceptions are echo and reverberation [86], in which delay characteristics are as important as magnitude characteristics.

When designing an ``instantaneous'' filtering operation, i.e., when not designing a ``delay effect'' such as an echo unit or reverberator, the amplitude response $G(\omega)$ should be as smooth as possible as a function of frequency $\omega$ . Smoother amplitude responses correspond to shorter impulse responses (when the phase is zero, linear, or ``minimum phase'' as discussed in the next chapter). By keeping impulse-responses as short as possible, phase dispersion is minimized, and ideally inaudible. Linearizing the phase response with a delay equalizer (a type of allpass filter) does not eliminate ringing, but merely shifts it in time. A general rule of thumb is to keep the total impulse-response duration below the time-discrimination threshold of hearing in the context of the intended application.

Next Section:
Minimum-Phase Filters
Previous Section:
Implementation Structures for Recursive Digital Filters

Filters Preserving Phase

Linear-Phase Filters
(Symmetric Impulse Responses)