Free Books    Introduction to Digital Filters  

Finding the Eigenstructure of A

Starting with the defining equation for an eigenvector $ \underline{e}$ and its corresponding eigenvalue $ \lambda$,

$\displaystyle A\underline{e}_i= \lambda_i \underline{e}_i,\quad i=1,2 $

we get

$\displaystyle \left[\begin{array}{cc} c & c-1 \\ [2pt] c+1 & c \end{array}\righ... ...egin{array}{c} \lambda_i \\ [2pt] \lambda_i \eta_i \end{array}\right]. \protect$ (G.23)

We normalized the first element of $ \underline{e}_i$ to 1 since $ g\underline{e}_i$ is an eigenvector whenever $ \underline{e}_i$ is. (If there is a missing solution because its first element happens to be zero, we can repeat the analysis normalizing the second element to 1 instead.)

Equation (G.23) gives us two equations in two unknowns:

$\displaystyle c+\eta_i (c-1)$ $\displaystyle =$ $\displaystyle \lambda_i \protect$ (G.24)
$\displaystyle (1+c) +c\eta_i$ $\displaystyle =$ $\displaystyle \lambda_i \eta_i$ (G.25)

Substituting the first into the second to eliminate $ \lambda_i $, we get

\begin{eqnarray*} 1+c+c\eta_i &=& [c+\eta_i (c-1)]\eta_i = c\eta_i + \eta_i ^2 (... ...-1)\\ \,\,\Rightarrow\,\,\eta_i &=& \pm \sqrt{\frac{c+1}{c-1}}. \end{eqnarray*}

Thus, we have found both eigenvectors

\begin{eqnarray*} \underline{e}_1&=&\left[\begin{array}{c} 1 \\ [2pt] \eta \end{... ...ght], \quad \hbox{where}\\ \eta&\isdef &\sqrt{\frac{c+1}{c-1}}. \end{eqnarray*}

They are linearly independent provided $ \eta\neq0\Leftrightarrow c\neq -1$ and finite provided $ c\neq 1$.

We can now use Eq.$ \,$(G.24) to find the eigenvalues:

$\displaystyle \lambda_i = c + \eta_i (c-1) = c \pm \sqrt{\frac{c+1}{c-1} (c-1)^2} = c \pm \sqrt{c^2-1} $

Assuming $ \left\vert c\right\vert<1$, the eigenvalues are

$\displaystyle \lambda_i = c \pm j\sqrt{1-c^2} \protect$ (G.26)

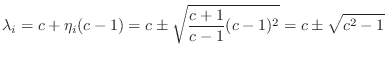
and so this is the range of $ c$ corresponding to sinusoidal oscillation. For $ \left\vert c\right\vert>1$, the eigenvalues are real, corresponding to exponential growth and decay. The values $ c=\pm 1$ yield a repeated root (dc or $ f_s/2$ oscillation).

Let us henceforth assume $ -1 < c < 1$. In this range $ \theta \isdef \arccos(c)$ is real, and we have $ c=\cos(\theta)$, $ \sqrt{1-c^2} = \sin(\theta)$. Thus, the eigenvalues can be expressed as follows:

\begin{eqnarray*} \lambda_1 &=& c + j\sqrt{1-c^2} = \cos(\theta) + j\sin(\theta)... ...- j\sqrt{1-c^2} = \cos(\theta) - j\sin(\theta) = e^{-j\theta}\\ \end{eqnarray*}

Equating $ \lambda_i $ to $ e^{j\omega_i T}$, we obtain $ \omega_i T = \pm \theta$, or $ \omega_i = \pm \theta/T = \pm f_s\theta = \pm f_s\arccos(c)$, where $ f_s$ denotes the sampling rate. Thus the relationship between the coefficient $ c$ in the digital waveguide oscillator and the frequency of sinusoidal oscillation $ \omega$ is expressed succinctly as

$\displaystyle \fbox{$\displaystyle c = \cos(\omega T).$} $

We see that the coefficient range (-1,1) corresponds to frequencies in the range $ (-f_s/2,f_s/2)$, and that's the complete set of available digital frequencies.

We have now shown that the system of Fig.G.3 oscillates sinusoidally at any desired digital frequency $ \omega$ rad/sec by simply setting $ c=\cos(\omega T)$, where $ T$ denotes the sampling interval.

Next Section:
Choice of Output Signal and Initial Conditions
Previous Section:
Jordan Canonical Form