Free Books    Introduction to Digital Filters  

Forward-Backward Filtering

There are no linear-phase recursive filters because a recursive filter cannot generate a symmetric impulse response. However, it is possible to implement a zero-phase filter offline using a recursive filter twice. That is, if the entire input signal $ x(\cdot)$ is stored in a computer memory or hard disk, for example, then we can apply a recursive filter both forward and backward in time. Doing this squares the amplitude response of the filter and zeros the phase response.

To show this analytically, let $ v(n)$ denote the output of the first filtering operation (which we'll take to be ``forward'' in time in the normal way), and let $ h(n)$ be the impulse response of the recursive filter. Then we have

$\displaystyle v(n) = (h\ast x)(n), $

where $ x(n)$ is the input signal at sample $ n$. For the second pass, we ``flip'' $ v(n)$ to obtain $ v(-n)$ and apply the filter again:

$\displaystyle w(n) = (h\ast$   FLIP$\displaystyle (v))(n) $

The final output is then this result flipped:

$\displaystyle y =$   FLIP$\displaystyle (w) =$   FLIP$\displaystyle (h\ast$   FLIP$\displaystyle (v)) =$   FLIP$\displaystyle (h)\ast v, $

where the last simplification tells us that flipping the input and output signals is equivalent to flipping the impulse response instead. Putting all these operations together, we have

$\displaystyle y(n) =$   FLIP$\displaystyle _n(h\ast$   FLIP$\displaystyle (h\ast x)) = ($FLIP$\displaystyle (h)\ast (h\ast x))(n). $

By the flip theorem for z transforms, we have that the z transform of FLIP$ (x)$ is $ X(z^{-1})$:

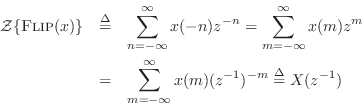
\begin{eqnarray*} {\cal Z}\{\mbox{{\sc Flip}}(x)\} &\isdef & \sum_{n=-\infty}^\i... ... &=& \sum_{m=-\infty}^\infty x(m) (z^{-1})^{-m} \isdef X(z^{-1}) \end{eqnarray*}

Using this result and applying the convolution theorem (§6.3) twice gives the z transform

$\displaystyle Y(z) = H(z^{-1})[H(z)X(z)]. $

On the unit circle, this reduces to, for real filters $ h$,

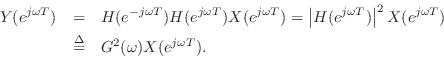
\begin{eqnarray*} Y(e^{j\omega T}) &=& H(e^{-j\omega T})H(e^{j\omega T})X(e^{j\o... ...rt^2 X(e^{j\omega T})\\ &\isdef & G^2(\omega) X(e^{j\omega T}). \end{eqnarray*}

If the filter were complex, then we would need to conjugate its coefficients when running it backwards.

In summary, we have thus shown that forward-backward filtering squares the amplitude response and zeros the phase response. Note also that the phase response is truly zero, never alternating between zero and $ \pi $. No matter what nonlinear phase response $ \Theta(\omega)$ a filter may have, this phase is completely canceled out by forward and backward filtering. The amplitude response, on the other hand, is squared. For simple bandpass filters (including lowpass, highpass, etc.), for which the desired gain is 1 in the passband and 0 in the stopband, squaring the amplitude response usually improves the response, because the ``stopband ripple'' (deviation from 0) is squared, thereby doubling the stopband attenuation in dB. On the other hand, passband ripple (deviation from 1) is only doubled by the squaring (because $ (1+\epsilon)^2 = 1+2\epsilon + \epsilon^2\approx 1+2\epsilon$).

A Matlab example of forward-backward filtering is presented in §11.6 (in Fig.11.1).

Next Section:
Phase Distortion at Passband Edges
Previous Section:
Antisymmetric Linear-Phase Filters