Free Books    Introduction to Digital Filters  

Linear-Phase Filters
(Symmetric Impulse Responses)

A linear-phase filter is typically used when a causal filter is needed to modify a signal's magnitude-spectrum while preserving the signal's time-domain waveform as much as possible. Linear-phase filters have a symmetric impulse response, e.g.,

$\displaystyle h(n) = h(N-1-n), \quad n=0,1,2,\ldots,N-1. $

The symmetric-impulse-response constraint means that linear-phase filters must be FIR filters, because a causal recursive filter cannot have a symmetric impulse response.

We will show that every real symmetric impulse response corresponds to a real frequency response times a linear phase term $ e^{-j\alpha\omega T}$, where $ \alpha = (N-1)/2$ is the slope of the linear phase. Linear phase is often ideal because a filter phase of the form $ \Theta(\omega) = - \alpha \omega T$ corresponds to phase delay

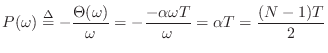
$\displaystyle P(\omega) \isdef - \frac{\Theta(\omega)}{\omega} = - \frac{-\alpha\omega T}{\omega} = \alpha T = \frac{(N-1)T}{2} $

and group delay

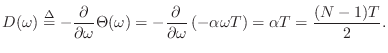
$\displaystyle D(\omega) \isdef - \frac{\partial}{\partial \omega}\Theta(\omega... ...l}{\partial \omega}\left(-\alpha\omega T\right) = \alpha T = \frac{(N-1)T}{2}. $

That is, both the phase and group delay of a linear-phase filter are equal to $ (N-1)/2$ samples of plain delay at every frequency. Since a length $ N$ FIR filter implements $ N-1$ samples of delay, the value $ (N-1)/2$ is exactly half the total filter delay. Delaying all frequency components by the same amount preserves the waveshape as much as possible for a given amplitude response.

Next Section:
Zero-Phase Filters (Even Impulse Responses)
Previous Section:
Pole-Zero Analysis Problems