DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Linearity

The Laplace transform is a linear operator. To show this, let $ w(t)$ denote a linear combination of signals $ x(t)$ and $ y(t)$,

$\displaystyle w(t) = \alpha x(t) + \beta y(t), $

where $ \alpha$ and $ \beta$ are real or complex constants. Then we have

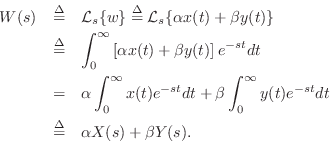
\begin{eqnarray*} W(s) &\isdef & {\cal L}_s\{w\} \isdef {\cal L}_s\{\alpha x(t) ... ..._0^\infty y(t) e^{-st} dt\\ &\isdef & \alpha X(s) + \beta Y(s). \end{eqnarray*}

Thus, linearity of the Laplace transform follows immediately from the linearity of integration.

Next Section:
Differentiation
Previous Section:
Paraunitary Filter Examples