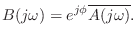Lossless Analog Filters
As discussed in §B.2, the an allpass filter can be defined
as any filter that preserves signal energy for every input
signal 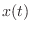 . In the continuous-time case, this means
. In the continuous-time case, this means
where
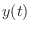
denotes the output signal, and
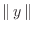
denotes the
L2 norm of

. Using the
Rayleigh energy theorem
(
Parseval's theorem) for
Fourier transforms [
87],
energy preservation can be expressed in the
frequency domain by
where
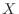
and
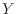
denote the Fourier transforms of

and

, respectively,
and frequency-domain L2
norms are defined by
If
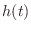
denotes the
impulse response of the
allpass
filter, then its
transfer function 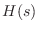
is given by the
Laplace transform of

,
and we have the requirement
Since this equality must hold for every input signal

, it must be
true in particular for complex
sinusoidal inputs of the form
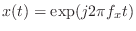
, in which case [
87]
where 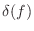 denotes the Dirac ``delta function'' or continuous
impulse function (§E.4.3). Thus, the allpass condition becomes
denotes the Dirac ``delta function'' or continuous
impulse function (§E.4.3). Thus, the allpass condition becomes
which implies
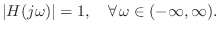 |
(E.15) |
Suppose

is a rational analog filter, so that
where
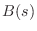
and
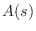
are polynomials in

:
(We have normalized 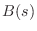 so that
so that 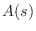 is monic (
is monic (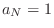 ) without
loss of generality.) Equation (E.15) implies
) without
loss of generality.) Equation (E.15) implies
If
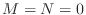
, then the allpass condition reduces to
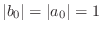
,
which implies
where
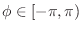
is any real phase constant. In other words,
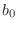
can be any unit-modulus
complex number. If
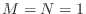
, then the
filter is allpass provided
Since this must hold for all

, there are only two solutions:
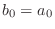 and
and 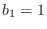 , in which case
, in which case
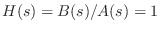 for all
for all  .
.
-
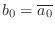 and
and 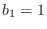 , i.e.,
, i.e.,
Case (1) is trivially allpass, while case (2) is the one discussed above
in the introduction to this section.
By analytic continuation, we have
If
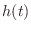
is real, then
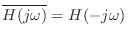
, and we can write
To have
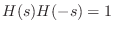
, every
pole at
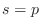
in
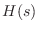
must be canceled
by a zero at
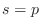
in

, which is a zero at
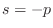
in
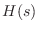
.
Thus, we have derived the simplified ``allpass rule'' for real analog
filters.
Next Section: State Space Filter Realization ExamplePrevious Section: Q as Energy Stored over Energy Dissipated![]() . In the continuous-time case, this means
. In the continuous-time case, this means
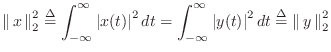
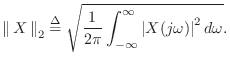
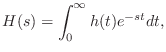
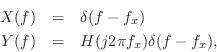
![]() denotes the Dirac ``delta function'' or continuous
impulse function (§E.4.3). Thus, the allpass condition becomes
denotes the Dirac ``delta function'' or continuous
impulse function (§E.4.3). Thus, the allpass condition becomes
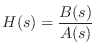
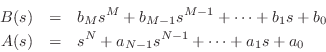
![]() so that
so that ![]() is monic (
is monic (![]() ) without
loss of generality.) Equation (E.15) implies
) without
loss of generality.) Equation (E.15) implies
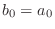 and
and 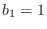 , in which case
, in which case
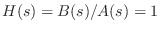 for all
for all  .
.
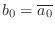 and
and 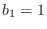 , i.e.,
, i.e.,