Matlab State-Space Filter Conversion Example
Here is the example of §F.6 repeated using matlab.G.9 The difference equation
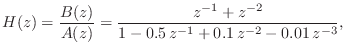
NUM = [0 1 1 0 ]; % NUM and DEN should be same length DEN = [1 -0.5 0.1 -0.01];The tf2ss function converts from ``transfer-function'' form to state-space form:
[A,B,C,D] = tf2ss(NUM,DEN) A = 0.00000 1.00000 0.00000 0.00000 0.00000 1.00000 0.01000 -0.10000 0.50000 B = 0 0 1 C = 0 1 1 D = 0
Next Section:
Diagonalizing a State-Space Model
Previous Section:
Other Relevant Matlab Functions




















