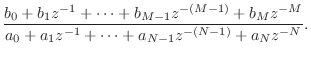Free Books    Introduction to Digital Filters  

Method

As can be seen from the code listing, this implementation of residuez simply calls residue, which was written to carry out the partial fraction expansions of $ s$-plane (continuous-time) transfer functions $ H(s)$:

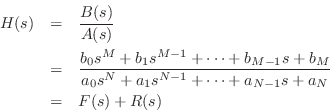
\begin{eqnarray*} H(s) &=& \frac{B(s)}{A(s)}\\ &=& \frac{b_0 s^M + b_1 s^{M-1}... ...s^N + a_1 s^{N-1} + \cdots + a_{N-1}s + a_N}\\ &=& F(s) + R(s) \end{eqnarray*}

where $ F(s)$ is the ``quotient'' and $ R(s)$ is the ``remainder'' in the PFE:

$\displaystyle F(s)$ $\displaystyle \isdef$ $\displaystyle f_0 s^L + f_1 s^{L-1} + \cdots + f_{L-1} s + f_L$  
$\displaystyle R(s)$ $\displaystyle \isdef$ $\displaystyle \frac{r_1}{(s-p_1)^m_1} + \cdots + \frac{r_N}{(s-p_N)^m_N} \protect$ (J.1)

where $ L=M-N$ is the order of the quotient polynomial in $ s$, and $ m_i$ is the multiplicity of the $ i$th pole. (When all poles are distinct, we have $ m_i=1$ for all $ i$.) For $ M<N$, we define $ F(s)=0$.

In the discrete-time case, we have the $ z$-plane transfer function

$\displaystyle H(z)$ $\displaystyle =$ $\displaystyle \frac{B(z)}{A(z)}$  
  $\displaystyle =$ $\displaystyle \frac{b_0 + b_1 z^{-1}+ \cdots + b_{M-1}z^{-(M-1)} + b_M z^{-M}} {a_0 + a_1 z^{-1}+ \cdots + a_{N-1}z^{-(N-1)} + a_N z^{-N}}. \protect$ (J.2)

For compatibility with Matlab's residuez, we need a PFE of the form $ H(z)=F(z)+R(z)$ such that

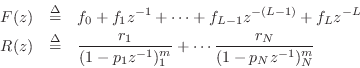
\begin{eqnarray*} F(z) &\isdef & f_0 + f_1 z^{-1}+ \cdots + f_{L-1} z^{-(L-1)} +... ...c{r_1}{(1-p_1z^{-1})^m_1} + \cdots \frac{r_N}{(1-p_Nz^{-1})^m_N} \end{eqnarray*}

where $ L=M-N$.

We see that the $ s$-plane case formally does what we desire if we treat $ z$-plane polynomials as polynomials in $ z^{-1}$ instead of $ z$. From Eq.$ \,$(J.2), we see that this requires reversing the coefficient-order of B and A in the call to residue. In the returned result, we obtain terms such as

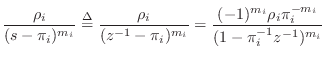
$\displaystyle \frac{\rho_i}{(s-\pi_i)^{m_i}} \isdef \frac{\rho_i}{(z^{-1}-\pi_i)^{m_i}} =\frac{(-1)^{m_i}\rho_i \pi_i^{-m_i}}{(1-\pi_i^{-1}z^{-1})^{m_i}} $

where the second form is simply the desired canonical form for $ z$-plane PFE terms. Thus, the $ i$th pole is

$\displaystyle p_i = \pi_i^{-1} $

and the $ i$th residue is

$\displaystyle r_i = \frac{\rho_i}{(-\pi_i)^{m_i}}. $

Finally, the returned quotient polynomial must be flipped for the same reason that the input polynomials needed to be flipped (to convert from left-to-right descending powers of $ z^{-1}$ [$ s$] in the returned result to ascending powers of $ z^{-1}$).

Next Section:
Example with Repeated Poles
Previous Section:
The Padé-Prony Method