Multi-Input, Multi-Output (MIMO)
Allpass Filters
To generalize lossless filters to the multi-input, multi-output (MIMO) case, we must generalize conjugation to MIMO transfer function matrices:
Theorem: A ![]() transfer function matrix
transfer function matrix
![]() is
lossless if and only if
its frequency-response matrix
is
lossless if and only if
its frequency-response matrix
![]() is unitary, i.e.,
is unitary, i.e.,
for all
Let
![]() denote the length
denote the length ![]() output vector at time
output vector at time ![]() , and
let
, and
let
![]() denote the input
denote the input ![]() -vector at time
-vector at time ![]() . Then in the
frequency domain we have
. Then in the
frequency domain we have
![]() , which
implies
, which
implies
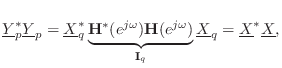
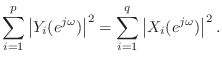
We have thus shown that in the MIMO case, losslessness is equivalent to having a unitary frequency-response matrix. A MIMO allpass filter is therefore any filter with a unitary frequency-response matrix.
Note that
![]() is a
is a ![]() matrix product
of a
matrix product
of a ![]() times a
times a ![]() matrix. If
matrix. If ![]() , then the rank
must be deficient. Therefore,
, then the rank
must be deficient. Therefore, ![]() . (There must be at least as
many outputs as there are inputs, but it's ok to have extra outputs.)
. (There must be at least as
many outputs as there are inputs, but it's ok to have extra outputs.)
Paraunitary MIMO Filters
In §C.2, we generalized the allpass property
![]() to the entire complex plane as
to the entire complex plane as
MIMO Paraconjugate
Definition:
The paraconjugate of
![]() is defined as
is defined as
![$\displaystyle \mathbf{H}(z)=\left[\begin{array}{c} 1+jz^{-1} \\ [2pt] 1+z^{-2} \end{array}\right]
$](http://www.dsprelated.com/josimages_new/filters/img1628.png)
MIMO Paraunitary Condition
With the above definition for paraconjugation of a MIMO transfer-function
matrix, we may generalize the MIMO allpass condition Eq.![]() (C.2) to the
entire
(C.2) to the
entire ![]() plane as follows:
plane as follows:
Theorem:
Every lossless ![]() transfer function matrix
transfer function matrix
![]() is paraunitary,
i.e.,
is paraunitary,
i.e.,
By construction, every paraunitary matrix transfer function is
unitary on the unit circle for all ![]() . Away from the
unit circle, the paraconjugate
. Away from the
unit circle, the paraconjugate
![]() is the unique analytic
continuation of
is the unique analytic
continuation of
![]() (the Hermitian transpose of
(the Hermitian transpose of
![]() ).
).
Example:
The normalized DFT matrix is an ![]() order zero
paraunitary transformation. This is because the normalized DFT
matrix,
order zero
paraunitary transformation. This is because the normalized DFT
matrix,
![]() , where
, where
![]() , is a
unitary matrix:
, is a
unitary matrix:
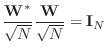
Properties of Paraunitary Systems
Paraunitary systems are essentially multi-input, multi-output (MIMO)
allpass filters. Let
![]() denote the
denote the ![]() matrix transfer
function of a paraunitary system. Some of its properties include the
following [98]:
matrix transfer
function of a paraunitary system. Some of its properties include the
following [98]:
- In the square case (
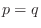 ), the matrix determinant,
), the matrix determinant,
![$ \det[\mathbf{H}(z)]$](http://www.dsprelated.com/josimages_new/filters/img1637.png) , is an allpass filter.
, is an allpass filter.
- Therefore, if a square
 contains FIR elements, its
determinant is a simple delay:
contains FIR elements, its
determinant is a simple delay:
![$ \det[\mathbf{H}(z)]=z^{-K}$](http://www.dsprelated.com/josimages_new/filters/img1638.png) for some
integer
for some
integer  .
.
Properties of Paraunitary Filter Banks
An ![]() -channel filter bank can be viewed as an
-channel filter bank can be viewed as an ![]() MIMO filter
MIMO filter
![$\displaystyle \mathbf{H}(z) = \left[\begin{array}{c} H_1(z) \\ [2pt] H_2(z) \\ [2pt] \vdots \\ [2pt] H_N(z)\end{array}\right]
$](http://www.dsprelated.com/josimages_new/filters/img1640.png)
A paraunitary filter bank must therefore obey
We can note the following properties of paraunitary filter banks:
- A synthesis filter bank
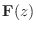 corresponding
to analysis filter bank
corresponding
to analysis filter bank
 is defined as that filter bank
which inverts the analysis filter bank, i.e., satisfies
Clearly, not every filter bank will be invertible in this way. When it is, it may be called a perfect reconstruction filter bank. When a filter bank transfer function
is defined as that filter bank
which inverts the analysis filter bank, i.e., satisfies
Clearly, not every filter bank will be invertible in this way. When it is, it may be called a perfect reconstruction filter bank. When a filter bank transfer function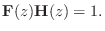
 is paraunitary, its
corresponding synthesis filter bank is simply the paraconjugate filter
bank
is paraunitary, its
corresponding synthesis filter bank is simply the paraconjugate filter
bank
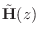 , or
, or

- The channel filters
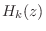 in a paraunitary filter bank
are power complementary:
This follows immediately from looking at the paraunitary property on the unit circle.
in a paraunitary filter bank
are power complementary:
This follows immediately from looking at the paraunitary property on the unit circle.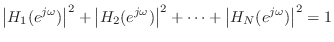
- When
 is FIR, the corresponding synthesis filter
matrix
is FIR, the corresponding synthesis filter
matrix
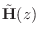 is also FIR. Note that this implies an FIR
filter-matrix can be inverted by another FIR filter-matrix. This is in
stark contrast to the case of single-input, single-output FIR filters,
which must be inverted by IIR filters, in general.
is also FIR. Note that this implies an FIR
filter-matrix can be inverted by another FIR filter-matrix. This is in
stark contrast to the case of single-input, single-output FIR filters,
which must be inverted by IIR filters, in general.
- When
 is FIR, each synthesis filter,
is FIR, each synthesis filter,
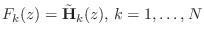 , is simply the
, is simply the 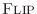 of its corresponding
analysis filter
of its corresponding
analysis filter
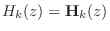 :
where
:
where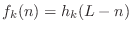
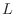 is the filter length. (When the filter coefficients are
complex,
is the filter length. (When the filter coefficients are
complex,  includes a complex conjugation as well.)
includes a complex conjugation as well.)
This follows from the fact that paraconjugating an FIR filter amounts to simply flipping (and conjugating) its coefficients.
Note that only trivial FIR filters can be paraunitary in the single-input, single-output (SISO) case. In the MIMO case, on the other hand, paraunitary systems can be composed of FIR filters of any order.
- FIR analysis and synthesis filters in paraunitary filter banks
have the same amplitude response.
This follows from the fact that
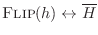 , i.e., flipping an FIR filter impulse response
, i.e., flipping an FIR filter impulse response  conjugates the frequency response, which does not affect its amplitude
response
conjugates the frequency response, which does not affect its amplitude
response
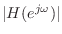 .
.
Paraunitary Filter Examples
The Haar filter bank is defined as
![$\displaystyle \mathbf{H}(z) = \frac{1}{\sqrt{2}}\left[\begin{array}{c} 1+z^{-1} \\ [2pt] 1-z^{-1} \end{array}\right]
$](http://www.dsprelated.com/josimages_new/filters/img1655.png)
![$\displaystyle {\tilde{\mathbf{H}}}(z) \mathbf{H}(z) = \left[\begin{array}{cc} 1...
...ight] \left[\begin{array}{c} 1+z^{-1} \\ [2pt] 1-z^{-1} \end{array}\right]
= 1
$](http://www.dsprelated.com/josimages_new/filters/img1657.png)
For more about paraunitary filter banks, see Chapter 6 of [98].
Next Section:
Allpass Problems
Previous Section:
Paraunitary FiltersC.4




















