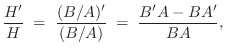DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Numerical Computation of Group Delay

The definition of group delay,

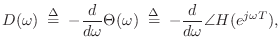
$\displaystyle D(\omega) \isdefs - \frac{d}{d\omega} \Theta(\omega) \isdefs - \frac{d}{d\omega} \angle H(e^{j\omega T}), $

does not give an immediately useful recipe for computing group delay numerically. In this section, we describe the theory of operation behind the matlab function for group-delay computation given in §J.8.

A more useful form of the group delay arises from the logarithmic derivative of the frequency response. Expressing the frequency response $ H(e^{j\omega T})$ in polar form as

$\displaystyle H(e^{j\omega T}) \isdefs G(\omega)e^{j\Theta(\omega)} $

yields the following logarithmic decomposition of magnitude and phase:

$\displaystyle \ln H(e^{j\omega T}) = \ln G(\omega) + j\Theta(\omega) $

Thus, the real part of the logarithm of the frequency response equals the log amplitude response, while the imaginary part equals the phase response.

Since differentiation is linear, the logarithmic derivative becomes

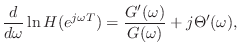
$\displaystyle \frac{d}{d\omega} \ln H(e^{j\omega T}) = \frac{G^\prime(\omega)}{G(\omega)} + j\Theta^\prime(\omega), $

where $ G^\prime(\omega)$ and $ \Theta^\prime(\omega)$ denote the derivatives of $ G(\omega)$ and $ \Theta(\omega)$, respectively, with respect to $ \omega$. We may therefore express the group delay as

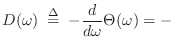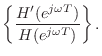
$\displaystyle D(\omega) \isdefs - \frac{d}{d\omega} \Theta(\omega) = -$im$\displaystyle \left\{\frac{d}{d\omega} \ln H(e^{j\omega T})\right\} = -$im$\displaystyle \left\{\frac{H^\prime(e^{j\omega T})}{H(e^{j\omega T})}\right\}. $

Consider first the FIR case in which $ H(z)=B(z)$, with

$\displaystyle B(z) \isdefs b_0 + b_1z^{-1}+ b_2z^{-2}+ \cdots + b_M z^{-M}. \protect$ (8.9)

In this case, the derivative is simply

\begin{eqnarray*} B^\prime(e^{j\omega T}) &\isdef & \frac{d}{d\omega}\left[b_0 ... ...b_M e^{-jM\omega T}\right]\\ &\isdef & -jT\,B_r(e^{j\omega T}), \end{eqnarray*}

where $ B_r(z)$ denotes ``$ B$ ramped'', i.e., the $ i$th coefficient of the polynomial $ B_r$ is $ i\,b_i$, for $ i=0,1,2,\ldots,M$. In matlab, we may compute Br from B via the following statement:

Br = B .* [0:M]; % Compute ramped B polynomial
The group delay of an FIR filter $ B(z)$ can now be written as

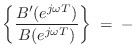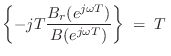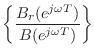
$\displaystyle D(\omega) \eqsp -$im$\displaystyle \left\{\frac{B^\prime(e^{j\omega T})}{B(e^{j\omega T})}\right\} \eqsp -$im$\displaystyle \left\{-jT\frac{B_r(e^{j\omega T})}{B(e^{j\omega T})}\right\} \eqsp T\,$re$\displaystyle \left\{\frac{B_r(e^{j\omega T})}{B(e^{j\omega T})}\right\} $

In matlab, the group delay, in samples, can be computed simply as
D = real(fft(Br) ./ fft(B))
where the fft, of course, approximates the Discrete Time Fourier Transform (DTFT). Such sampling of the frequency axis by this approximation is information-preserving whenever the number of samples (FFT length) exceeds the polynomial order $ M$. The ratio of sampled DTFTs, however, is undersampled, in general. In fact, we may have $ B(e^{j\omega T})=0$ at some frequencies (``zeros on the unit circle''). The grpdelay matlab utility in §J.8 watches out for division by zero, and simply sets the group delay to zero at such frequencies. Note that the true group delay approaches infinite magnitude as either a zero or pole approaches the unit circle.

Finally, when there are both poles and zeros, we have

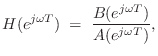
$\displaystyle H(e^{j\omega T}) \eqsp \frac{B(e^{j\omega T})}{A(e^{j\omega T})}, $

where $ B(e^{j\omega T})$ is given in Eq.$ \,$(7.9), and

$\displaystyle A(z) \isdefs 1 + a_1z^{-1}+ a_2z^{-2}+ \cdots + a_N z^{-N}. \protect$ (8.10)

Straightforward differentiation yields

$\displaystyle \frac{H^\prime}{H} \eqsp \frac{(B/A)^\prime}{(B/A)} \eqsp \frac{B^\prime A - B A^\prime}{BA}, \protect$ (8.11)

and this can be implemented analogous to the FIR case discussed above. However, a faster algorithm (usually) results from converting the IIR case to the FIR case:

$\displaystyle C(z) \isdefs B(z)\left[ z^{-N}\overline{A}(1/z)\right] \isdefs B(z)\tilde{A}(z) \protect$ (8.12)

where

$\displaystyle \tilde{A}(z)\isdefs z^{-N}\overline{A}(1/z) \eqsp [\overline{a}_... ..._{N-1}z^{-1},\overline{a}_{N-2}z^{-2},\ldots,\overline{a}_1 z^{-(N-1)}+z^{-N}] $

may be called the ``flip-conjugate'' or ``Hermitian conjugate'' of the polynomial $ A(z)$.8.4In matlab, the C polynomial is given by
C = conv(B,fliplr(conj(A)));
It is straightforward to show (Problem 11) that

$\displaystyle \angle\tilde{A}(e^{j\omega T}) \eqsp -\angle A(e^{j\omega T}) - N\omega T. $

The phase of the IIR filter $ H(z)=B(z)/A(z)$ is therefore

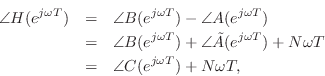
\begin{eqnarray*} \angle H(e^{j\omega T}) &=& \angle B(e^{j\omega T}) - \angle ... ...mega T}) + N\omega T\\ &=& \angle C(e^{j\omega T}) + N\omega T, \end{eqnarray*}

and the group delay computation thus reduces to the FIR case:

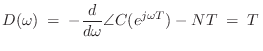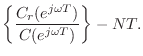
$\displaystyle D(\omega) \eqsp - \frac{d}{d\omega} \angle C(e^{j\omega T}) - NT \eqsp T\,$re$\displaystyle \left\{\frac{C_r(e^{j\omega T})}{C(e^{j\omega T})}\right\} - NT. $

This method is implemented in §J.8.

Next Section:
Computing Reflection Coefficients to Check Filter Stability
Previous Section:
Vocoder Analysis