DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

PFE to Real, Second-Order Sections

When all coefficients of $ A(z)$ and $ B(z)$ are real (implying that $ H(z)=B(z)/A(z)$ is the transfer function of a real filter), it will always happen that the complex one-pole filters will occur in complex conjugate pairs. Let $ (r,p)$ denote any one-pole section in the PFE of Eq.$ \,$(6.7). Then if $ p$ is complex and $ H(z)$ describes a real filter, we will also find $ (\overline{r},\pc)$ somewhere among the terms in the one-pole expansion. These two terms can be paired to form a real second-order section as follows:

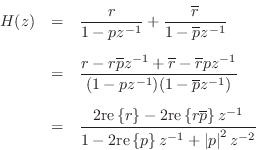
\begin{eqnarray*} H(z) &=& \frac{r}{1-pz^{-1}} + \frac{\overline{r}}{1-\pc z^{-1... ...box{re}\left\{p\right\}z^{-1}+ \left\vert p\right\vert^2 z^{-2}} \end{eqnarray*}

Expressing the pole $ p$ in polar form as $ p=Re^{j\theta}$, and the residue as $ r=Ge^{j\phi}$, the last expression above can be rewritten as

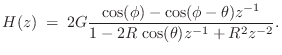
$\displaystyle H(z) \eqsp 2G\frac{\cos(\phi)-\cos(\phi-\theta)z^{-1}}{1-2R\,\cos(\theta)z^{-1}+ R^2 z^{-2}}. $

The use of polar-form coefficients is discussed further in the section on two-pole filters (§B.1.3).

Expanding a transfer function into a sum of second-order terms with real coefficients gives us the filter coefficients for a parallel bank of real second-order filter sections. (Of course, each real pole can be implemented in its own real one-pole section in parallel with the other sections.) In view of the foregoing, we may conclude that every real filter with $ M<N$ can be implemented as a parallel bank of biquads.7.6 However, the full generality of a biquad section (two poles and two zeros) is not needed because the PFE requires only one zero per second-order term.

To see why we must stipulate $ M<N$ in Eq.$ \,$(6.7), consider the sum of two first-order terms by direct calculation:

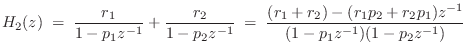$\displaystyle H_2(z) \eqsp \frac{r_1}{1-p_1z^{-1}} + \frac{r_2}{1-p_2z^{-1}} \eqsp \frac{(r_1 + r_2) - (r_1 p_2 + r_2 p_1) z^{-1}}{(1-p_1z^{-1})(1-p_2z^{-1})}$ (7.9)

Notice that the numerator order, viewed as a polynomial in $ z^{-1}$, is one less than the denominator order. In the same way, it is easily shown by mathematical induction that the sum of $ N$ one-pole terms $ r_i/(1-p_i z^{-1})$ can produce a numerator order of at most $ M=N-1$ (while the denominator order is $ N$ if there are no pole-zero cancellations). Following terminology used for analog filters, we call the case $ M<N$ a strictly proper transfer function.7.7 Thus, every strictly proper transfer function (with distinct poles) can be implemented using a parallel bank of two-pole, one-zero filter sections.

Next Section:
Inverting the Z Transform
Previous Section:
Complex Example