DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Phase Response

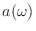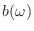Now we may isolate the filter phase response $ \Theta(\omega)$ by taking a ratio of the $ a(\omega)$ and $ b(\omega)$ in Eq.$ \,$(1.5):

\begin{eqnarray*} \frac{b(\omega)}{a(\omega)} &=& -\frac{G(\omega) \sin\left[\... ...eft[\Theta(\omega)\right]}\\ &\isdef & - \tan[\Theta(\omega)] \end{eqnarray*}

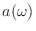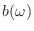Substituting the expansions of $ a(\omega)$ and $ b(\omega)$ yields

\begin{eqnarray*} \tan[\Theta(\omega)] &=& - \frac{b(\omega)}{a(\omega)} \\ &=&... ...n(\omega T/2)}{\cos(\omega T/2)} = \tan\left(-\omega T/2\right). \end{eqnarray*}

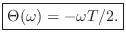
Thus, the phase response of the simple lowpass filter $ y(n) = x(n) + x(n - 1)$ is

$\displaystyle \zbox {\Theta(\omega) = -\omega T/2.} \protect$ (2.7)

We have completely solved for the frequency response of the simplest low-pass filter given in Eq.$ \,$(1.1) using only trigonometric identities. We found that an input sinusoid of the form

$\displaystyle x(n) = A \cos(2\pi fnT + \phi) $

produces the output

$\displaystyle y(n) = 2A \cos(\pi f T) \cos(2\pi fnT + \phi - \pi fT). $

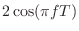
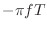
Thus, the gain versus frequency is $ 2\cos(\pi fT)$ and the change in phase at each frequency is given by $ -\pi fT$ radians. These functions are shown in Fig.1.7. With these functions at our disposal, we can predict the filter output for any sinusoidal input. Since, by Fourier theory [84], every signal can be represented as a sum of sinusoids, we've also solved the more general problem of predicting the output given any input signal.

Next Section:
Complex Sinusoids
Previous Section:
Amplitude Response