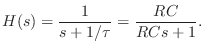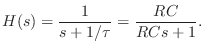Poles and Zeros

In the simple RC-filter example of §E.4.3, the transfer function is

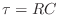
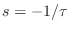
Thus, there is a single pole at , and we can say there is one zero at infinity as well. Since resistors and capacitors always have positive values, the time constant is always non-negative. This means the impulse response is always an exponential decay--never a growth. Since the pole is at , we find that it is always in the left-half plane. This turns out to be the case also for any complex analog one-pole filter. 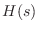By consideration of the partial fraction expansion of any , it is clear that, for stability of an analog filter, all poles must lie in the left half of the complex plane. This is the analog counterpart of the requirement for digital filters that all poles lie inside the unit circle.

---

Next Section:
Driving Point Impedance
Previous Section:
The Continuous-Time Impulse

Sign in