DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Q as Energy Stored over Energy Dissipated

Yet another meaning for $ Q$ is as follows [20, p. 326]

$\displaystyle Q = 2\pi\frac{\hbox{Stored Energy}}{\hbox{Energy Dissipated in One Cycle}} $

where the resonator is freely decaying (unexcited).

Proof. The total stored energy at time $ t$ is equal to the total energy of the remaining response. After an impulse at time 0, the stored energy in a second-order resonator is

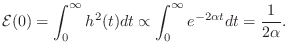
$\displaystyle {\cal E}(0) = \int_0^\infty h^2(t)dt \propto \int_0^\infty e^{-2\alpha t}dt = \frac{1}{2\alpha}. $

The energy dissipated in the first period $ P = 2\pi/\omega_p$ is $ {\cal E}(0)-{\cal E}(P)$, where

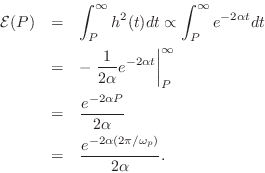
\begin{eqnarray*} {\cal E}(P) &=& \int_P^\infty h^2(t)dt \propto \int_P^\infty e... ...}}{2\alpha}\\ &=& \frac{e^{-2\alpha (2\pi/\omega_p)}}{2\alpha}. \end{eqnarray*}

Assuming $ Q\gg 1/2$ as before, $ \omega_p\approx\omega_0$ so that

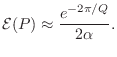
$\displaystyle {\cal E}(P) \approx \frac{e^{-2\pi/Q}}{2\alpha}. $

Assuming further that $ Q\gg 2\pi$, we obtain

$\displaystyle {\cal E}(0)-{\cal E}(P) \approx \frac{1}{2\alpha} \left(1-e^{-\frac{2\pi}{Q}}\right) \approx \frac{1}{2\alpha}\frac{2\pi}{Q}. $

This is the energy dissipated in one cycle. Dividing this into the total stored energy at time zero, $ {\cal E}(0)=1/(2\alpha)$, gives

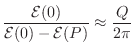
$\displaystyle \frac{{\cal E}(0)}{{\cal E}(0)-{\cal E}(P)} \approx \frac{Q}{2\pi} $

whence

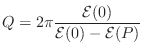
$\displaystyle Q = 2\pi \frac{{\cal E}(0)}{{\cal E}(0)-{\cal E}(P)} $

as claimed. Note that this rule of thumb requires $ Q\gg 2\pi$, while the one of the previous section only required $ Q\gg 1/2$.

Next Section:
Lossless Analog Filters
Previous Section:
Decay Time is Q Periods