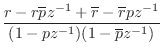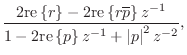Free Books    Introduction to Digital Filters  

Real Second-Order Sections

In practice, however, signals are typically real-valued functions of time. As a result, for real filters (§5.1), it is typically more efficient computationally to combine complex-conjugate one-pole sections together to form real second-order sections (two poles and one zero each, in general). This process was discussed in §6.8.1, and the resulting transfer function of each second-order section becomes

$\displaystyle \frac{r}{1-pz^{-1}} + \frac{\overline{r}}{1-\pc z^{-1}}$ $\displaystyle =$ $\displaystyle \frac{r-r\pc z^{-1}+\overline{r}-\overline{r}pz^{-1}}{(1-pz^{-1})(1-\pc z^{-1})}$  
  $\displaystyle =$ $\displaystyle \frac{2\mbox{re}\left\{r\right\}-2\mbox{re}\left\{r\pc\right\}z^{... ...-2\mbox{re}\left\{p\right\}z^{-1} + \left\vert p\right\vert^2 z^{-2}}, \protect$ (10.3)

where $ p$ is one of the poles, and $ r$ is its corresponding residue. This is a special case of the biquad section discussed in §B.1.6.

When the two poles of a real second-order section are complex, they form a complex-conjugate pair, i.e., they are located at $ z=R\exp(\pm j\theta)$ in the $ z$ plane, where $ R=\vert p\vert$ is the modulus of either pole, and $ \theta$ is the angle of either pole. In this case, the ``resonance-tuning coefficient'' in Eq.$ \,$(9.3) can be expressed as

$\displaystyle 2$$\displaystyle \mbox{re\ensuremath{\left\{p\right\}}}$$\displaystyle = 2R\cos(\theta) $

which is often more convenient for real-time control of resonance tuning and/or bandwidth. A more detailed derivation appears in §B.1.3.

Figures 3.25 and 3.26 (p. [*]) illustrate filter realizations consisting of one first-order and two second-order filter sections in parallel.

Next Section:
Implementation of Repeated Poles
Previous Section:
First-Order Complex Resonators