Series Case
Figure 6.1 illustrates the series connection of two
filters
![]() and
and
![]() .
The output
.
The output ![]() from filter 1 is used as the input to filter 2.
Therefore, the overall transfer function is
from filter 1 is used as the input to filter 2.
Therefore, the overall transfer function is
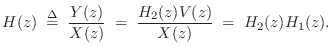
Next Section:
Parallel Case
Previous Section:
Convolution Theorem




















